1.1 Introduction
One of the most important uses of vector analysis (cf. Appendix A) is in the concise formulation of physical laws and the derivation of other results from these laws. We will develop and use the differential equations of motion for a body moving under the influence of a gravitational force only. In Chap. , we will add other (perturbing) forces to our model.
There are related disciplines, which are part of Flight Dynamics.
Def. : Celestial Mechanics is the study of the natural motion of celestial bodies.
Def. : Astrodynamics is the study of the controlled flight paths of spacecraft.
Def.: Orbital Mechanics is the study of the principles governing the motion of bodies around other bodies under the influence of gravity and other forces.
These subjects consider translational motion in a gravity field.
Attitude Dynamics and Attitude Control consider the spacecrafts rotational motion about its center of mass.
Def. : Spacecraft attitude dynamics is the applied science whose aim is to understand and predict how the spacecrafts orientation evolves.
In spacecraft mission activities, there is a coupling between satellite translation (the orbital variables) and spacecraft rotation (the attitude variables). In spite of the coupling effects, much of orbital mechanics proceeds by largely ignoring the effects of spacecraft attitude dynamics and vice versa. The field of Flight Dynamics, however, considers 6 degrees of freedom (DOF), consisting of 3 DOF from Orbital Mechanics and 3 DOF from Attitude Dynamics.
An example of an essentially 6DOF problem is: EDL (entry, descent, and landing), e.g., the landing of the Phoenix spacecraft on Mars 5/25/08. More information on the Phoenix mission can be found at the Phoenix Mars Mission Website at http://phoenix.lpl.arizona.edu/ .
Parallel disciplines that must be part of spacecraft mission analyses include:
Orbital Mechanics | Attitude Dynamics |
Orbit Determination | Attitude Determination |
Flight Path Control | Attitude Control |
Of these six disciplines, we consider primarily Orbital Mechanics plus related issues in Flight Path Control. Hence, our objective is to study the controlled flight paths of spacecraft, viz., Astrodynamics.
1.2 Mathematical Models
Use of Mathematical Models to Solve Physical Problems
Figure describes the procedure for using a mathematical model to solve a physical problem.
Fig. 1.1
Using a mathematical model to solve physical problems
In engineering, we make simplifying assumptions in our mathematical model to:
Get a good approximation to a solution
Gain insight into the problem
Get a good starting point for a more accurate numerical solution
Reduce computing time and costs.
Example: Archimedes
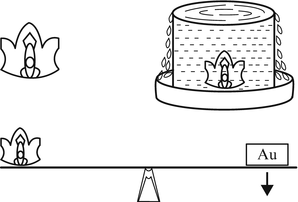
The king told Archimedes that he had given the goldsmith gold to make a crown for him. However, he suspected that the goldsmith had kept some of the gold and added a baser metal in its place. So his task for Archimedes was to determine whether or not his new crown was made of pure gold. Archimedes thought about this problem until one day when he was in the public bath and he saw water splashing out of a bathtub. Then, he yelled Eureka and ran to his working area to demonstrate the answer to the problem.
He placed the crown in a vat filled with water with a basin below the vat to catch the overflow. He obtained the amount of gold that equaled the volume of water that overflowed the vat. Then he placed this amount of gold on one side of a lever and the crown on the other side as shown in Fig.. The end of the lever with the gold descended, indicating that the crown was not pure gold. After Archimedes reported his findings to the king, the goldsmith did not cheat any more kings.
Fig. 1.2
Archimedes Gold Experiment
Dynamics, including Astrodynamics, is a deductive discipline, which enables us:
To describe in quantitative terms how mechanical systems move when acted on by given forces or
To determine which forces must be applied to a system to cause it to move in a specified manner.
A dynamics problem is solved in two major steps:
Formulation of the equation of motion (EOM), the math model, and
Extraction of information from the EOM.
Optimization of rocket trajectories is usually accomplished by analytical and numerical approaches in a complimentary fashion. Dereck Lawden (cf. reference for Lawden) says; by making suitable simplifying assumptions, the actual problem can be transformed into an idealized problem whose solution is analytically tractable, then this latter solution will often provide an excellent substitute for the optimal motor thrust programme in the actual situation. All that then remains to be done is to recompute the trajectory employing this programme and taking account of the real circumstances. Further, it is only by adopting the analytical approach in any field of research, that those general principles, which lead to a real understanding of the nature of the solutions, are discovered. Lacking such an appreciation, our sense of direction for the numerical attack will be defective and, as a consequence, computations will become unnecessarily lengthy or even quite ineffective.
The analytical solution provides insight into how to approach a problem. It also enables you to verify that your solution is plausible and correct. You do not want to put yourself in the position of having your boss tell you that the results you have presented violate a basic principle and then be forced to say, But the computer said . Another reason for looking at an idealized problem is that the insight gained can be used for mission planning and design purposes or feasibility studies for which exact values are not available.
High-precision software run in land-based computers or powerful real-time onboard computing provide precision numerical results and ultimately the commands to be executed by the spacecrafts onboard subsystems.
Coordinate Systems
To study motion, we need to set up a reference frame because we need to know motion with respect to what?
Inertial frames are fixed with respect to the fixed stars, i.e., non-rotating and non-accelerating with respect to the fixed (from our perspective) stars, which is an imaginary situation. Practically speaking, an inertial system is moving with essentially constant velocity.
Example
Geocentric equatorial system or Earth-centered Inertial (ECI) coordinate system
Use: To study orbital motion about the Earth
Definition:
Origin at the center of the earth
X-axis pointing to the first point of Aries, i.e., the vernal equinox. The vernal equinox direction is a directed line from the earth to the sun at the instant the sun passes through the earths equatorial plane at the beginning of spring.