Iaco Veris - Practical Astrodynamics

Practical Astrodynamics — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Practical Astrodynamics" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...352

Springer International Publishing AG 2018

Alessandro de Iaco Veris Practical Astrodynamics Springer Aerospace Technology

1. The Two-Body Problem

Alessandro de Iaco Veris 1

(1)

Rome, Italy

Alessandro de Iaco Veris

Email:

1.1 Position of the Problem

Astrodynamics is defined by Kaplan [] as the determination, prediction, physical adjustment, and optimisation of trajectories in space; space navigation and mission analysis; perturbation theories and expansions; spacecraft attitude dynamics and estimation. These topics and the mathematical methods used to solve practical problems arising in them form the subject of the present book. Some authors separate astrodynamics from celestial mechanics, by limiting the scope of the latter to the motion of natural celestial bodies, which is not under human control. However, the motion of all celestial bodies, be they natural or artificial, is governed by the same laws of mechanics.

This introductory chapter is meant to provide the reader with the basic concepts of the two-body problem, which consists in determining the motion of two isolated bodies, of masses, respectively, m 1 and m 2, attracting each other with Newtonian gravitational forces whose magnitude is directly proportional to the product m 1 m 2 and inversely proportional to the square of the distance between the two bodies. In other words, given at an initial time the positions and velocities of two isolated bodies acted upon only by their mutual gravitational attraction, it is required to determine their positions and velocities at any other time.

As is well known, the solution of this problem is governed by Keplers laws of planetary motion, which are given below.

1. The orbits of the planets around the Sun are ellipses, with the Sun at one focus.

   
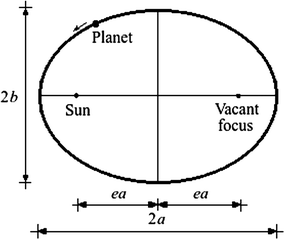
2. The radius vector of each planet (i.e., the straight line segment drawn from the Sun to that planet) sweeps out equal areas in equal times, as the planet travels along its orbit.

   

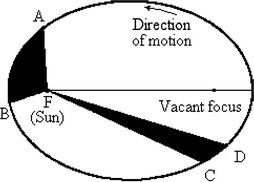   In the figure shown above, the time t AB taken by a planet to go from A to B is the same as the time t CD taken by the same planet to go from C to D, because the area of the sector FAB is equal to the area of the sector FCD. Thus, a planet moves fastest along its orbit when it is in the region about perihelion, and most slowly when it is near aphelion. For the sake of clearness, the figures given above show an ellipse having an eccentricity of about 0.68, which value is much higher than that of the orbit of any planet revolving around the Sun. The real eccentricities of the planetary orbits are generally small, as shown in the following table.

   Planetary eccentricities

   Mercury	0.205	Jupiter	0.049
   Venus	0.007	Saturn	0.057
   Earth	0.017	Uranus	0.046
   Mars	0.094	Neptune	0.011

   Courtesy of NASA []
3. The ratio of the squares of the periods T 1 and T 2 of revolution for two planets is equal to the ratio of the cubes of their respective major semi-axes a 1 and a 2, that is,

   

As will be shown in Sect. , the third law implies that the period, T , of a planet, which revolves around the Sun along an elliptic orbit, depends only on the size of the major semi-axis, a , of the ellipse, that is,

where = GM = 1.327 1011 km3/s2 is the gravitational parameter of the Sun, G = 6.673 1020 km3/(kg s2) is the universal gravitational constant, and M is the mass of the Sun. This also means that the mean orbital speed is lower for the planets orbiting far away from the Sun than for those orbiting near it, as shown in the following table.

Mean orbital speeds (km/s) of the planets

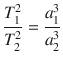
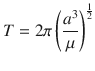
Mercury	47.4	Jupiter	13.1
Venus	35.0	Saturn	9.7
Earth	29.8	Uranus	6.8
Mars	24.1	Neptune	5.4

Courtesy of NASA []

Johannes Kepler found these laws (the first two in 1609 and the third in 1619) in an effort to fit various geometrical curves to the astronomical observations performed by Tycho Brahe on the orbit of Mars. In 1609, Kepler found that the data supplied by Brahe could be explained if the path followed by Mars were an ellipse having the Sun at one focus. The two-body model used by Kepler to describe the motion of the planets around the Sun is valid, because the gravitational attraction exerted by the Sun on the planets overcomes all other forces acting on them by several orders of magnitude.

As has been shown at length by several authors (see for example Hyman []:

1. Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare (Every body remains in its state of rest or of uniform motion in a straight line, unless it is compelled to change that state by forces impressed upon it). This law was originally enunciated by Galileo in 1638 [] in the following terms Inoltre, lecito aspettarsi che, qualunque grado di velocit si trovi in un mobile, gli sia per sua natura indelebilmente impresso, purch siano tolte le cause esterne di accelerazione o di ritardamento; il che accade soltanto nel piano orizzontale and is also known as the law of inertia.
2. Mutationem motus proportionalem esse vi motrici impress, & fieri secundum lineam rectam qua vis illa imprimitur (The rate of change of momentum is proportional to the motive force impressed and is directed along the straight line in which that force is impressed), that is,

   

   where m is the mass of the body considered, and f and v are, respectively, the resultant of the forces applied to the body and its velocity vector. In case of constant mass, the preceding expression reduces to

   

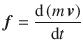   where a = d v /dt is the acceleration vector applied to the body.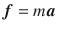
3. Actioni contrariam semper & qualem esse reactionem: sive corporum duorum actiones in se mutuo semper esse quales & in partes contrarias dirigi (To every action there is always opposed an equal reaction, that is, the mutual actions exerted by two bodies are always equal and oppositely directed).

To show how Keplers laws on planetary orbits follow from Newtons laws, let us make the following assumptions for the two-body problem:

Next page

1234567...352

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Practical Astrodynamics»

Look at similar books to Practical Astrodynamics. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Gary T. Henry

Practical Sampling

Jennifer Johnson

Montessori Practical Life: A Guide to Developing Independence, Confidence and a Sense of Responsibility in Children Using Montessori Practical Life

Tim Nyberg

The Practical Jokers Handbook: The Sequel

Dorothy C. Bass

Christian Practical Wisdom: What It Is, Why It Matters

Ron Lenk

Practical Lighting Design with LEDs

Jonsson

Practical Boating Knots: How to tie the +25 most practical rope knots and master them

Hintz

Orbital Mechanics and Astrodynamics

Valentin Nicolescu

Practical Guide to SAP NetWeaver PI - Development

Chaganti

Xen Virtualization: a Practical Handbook

Wilson

Introducing Body Language : a Practical Guide

Husain A.

Practical Epilepsy

Eric W. Skopec

The Practical Executive and Team-Building (Practical Executive Series)

Discussion, reviews of the book Practical Astrodynamics and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.