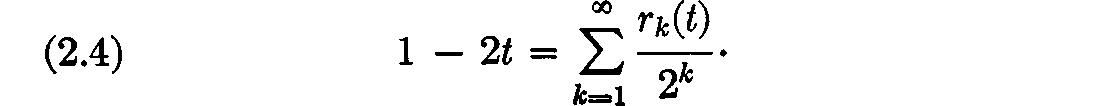Bibliographical Note This Dover edition, first published in 2018, is an unabridged republication of the work originally printed by the Mathematical Association of America, Washington, DC, 1959, as Number 12 in The Carus Mathematical Monographs series. International Standard Book NumberISBN-13: 978-0-486-82158-0ISBN-10: 0-486-82158-7 Manufactured in the United States by LSC Communications 82158701 2018 www.doverpublications.com TO MY TEACHERPROFESSOR HUGO STEINHAUS PREFACE At the meeting of the Mathematical Association of America held in the Summer of 1955, I had the privilege of delivering the Hedrick Lectures. I was highly gratified when, sometime later, Professor T. Rado, on behalf of the Committee on Carus Monographs, kindly invited me to expand my lectures into a monograph. At about the same time I was honored by an invitation from Haverford College to deliver a series of lectures under the Philips Visitors Program. This invitation gave me an opportunity to try out the projected monograph on a "live" audience, and this book is a slightly revised version of my lectures delivered at Haverford College during the Spring Term of 1958.
Bibliographical Note This Dover edition, first published in 2018, is an unabridged republication of the work originally printed by the Mathematical Association of America, Washington, DC, 1959, as Number 12 in The Carus Mathematical Monographs series. International Standard Book NumberISBN-13: 978-0-486-82158-0ISBN-10: 0-486-82158-7 Manufactured in the United States by LSC Communications 82158701 2018 www.doverpublications.com TO MY TEACHERPROFESSOR HUGO STEINHAUS PREFACE At the meeting of the Mathematical Association of America held in the Summer of 1955, I had the privilege of delivering the Hedrick Lectures. I was highly gratified when, sometime later, Professor T. Rado, on behalf of the Committee on Carus Monographs, kindly invited me to expand my lectures into a monograph. At about the same time I was honored by an invitation from Haverford College to deliver a series of lectures under the Philips Visitors Program. This invitation gave me an opportunity to try out the projected monograph on a "live" audience, and this book is a slightly revised version of my lectures delivered at Haverford College during the Spring Term of 1958.
My principal aim in the original Hedrick Lectures, as well as in this enlarged version, was to show that (a) extremely simple observations are often the starting point of rich and fruitful theories and (b) many seemingly unrelated developments are in reality variations on the same simple theme. Except for the last chapter where I deal with a spectacular application of the ergodic theorem to continued fractions, the book is concerned with the notion of statistical independence. This notion originated in probability theory and for a long time was handled with vagueness which bred suspicion as to its being a bona fide mathematical notion. We now know how to define statistical independence in most general and abstract terms. But the modern trend toward generality and abstraction tended not only to submerge the simplicity of the underlying idea but also to obscure the possibility of applying probabilistic ideas outside the field of probability theory. In the pages that follow, I have tried to rescue statistical independence from the fate of abstract oblivion by showing how in its simplest form it arises in various contexts cutting across different mathematical disciplines.
As to the preparation of the reader, I assume his familiarity with Lebesgue's theory of measure and integration, elementary theory of Fourier integrals, and rudiments of number theory. Because I do not want to assume much more and in order not to encumber the narrative by too many technical details I have left out proofs of some statements. I apologize for these omissions and hope that the reader will become sufficiently interested in the subject to fill these gaps by himself. I have appended a small bibliography which makes no pretence at completeness. Throughout the book I have also put in a number of problems. These problems are mostly quite difficult, and the reader should not feel discouraged if he cannot solve them without considerable effort.
I wish to thank Professor C. O. Oakley and R. J. Wisner of Haverford College for their splendid cooperation and for turning the chore of traveling from Ithaca to Haverford into a real pleasure. I was fortunate in having as members of my audience Professor H.
Rademacher of the University of Pennsylvania and Professor John Oxtoby of Bryn Mawr College. Their criticism, suggestions, and constant encouragement have been truly invaluable, and my debt to them is great. My Cornell colleagues, Professors H. Widom and M. Schreiber, have read the manuscript and are responsible for a good many changes and improvements. It is a pleasure to thank them for their help.
My thanks go also to the Haverford and Bryn Mawr undergraduates, who were the "guinea pigs," and especially to J. Reill who compiled the bibliography and proofread the manuscript. Last but not least, I wish to thank Mrs. Axelsson of Haverford College and Miss Martin of the Cornell Mathematics Department for the often impossible task of typing the manuscript from my nearly illegible notes. MARK KAC Ithaca, New YorkSeptember, 1959 CONTENTS STATISTICAL INDEPENDENCE IN PROBABILITY, ANALYSIS & NUMBER THEORY CHAPTER FROM VIETA TO THE NOTION OF STATISTICAL INDEPENDENCE . A formula of Vieta. We start from simple trigonometry.
Write 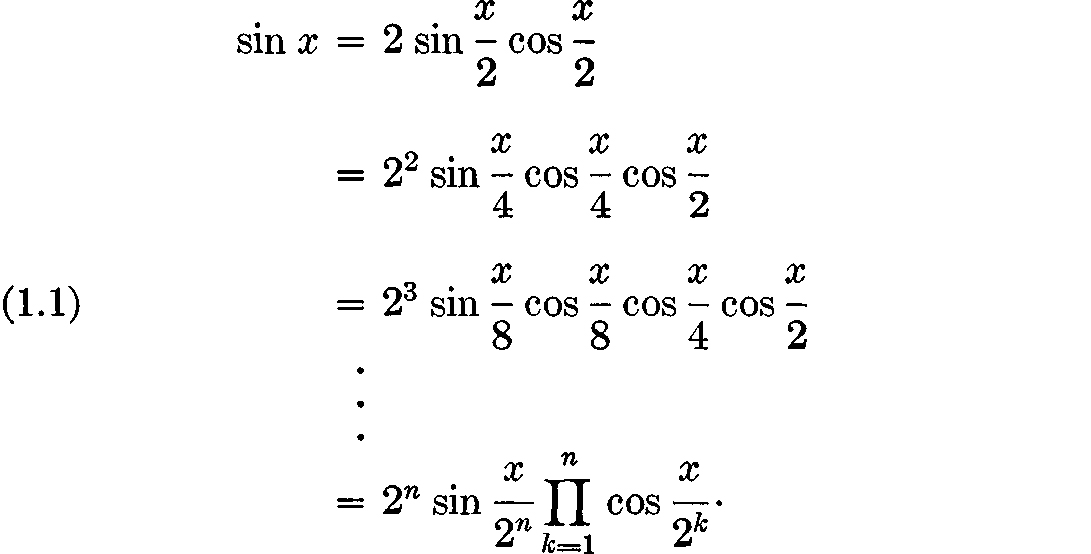 From elementary calculus we know that, for x 0,
From elementary calculus we know that, for x 0, 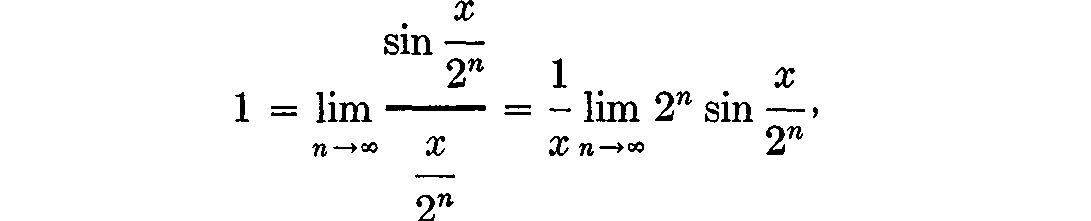 and hence
and hence 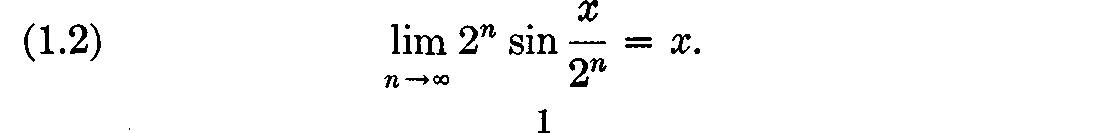 ), we get
), we get 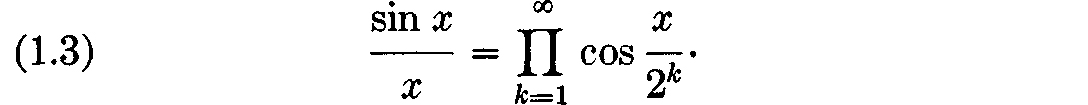 A special case of () is of particular interest. Setting x = /2, we obtain
A special case of () is of particular interest. Setting x = /2, we obtain 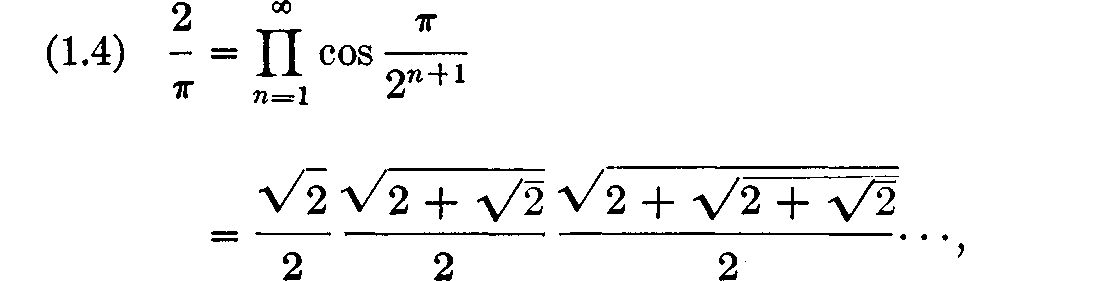 a classical formula due to Vieta. . Another look at Vieta's formula. So far everything has been straightforward and familiar. Now let us take a look at () from a different point of view. It is known that every real number t, 0 t 1, can be written uniquely in the form
a classical formula due to Vieta. . Another look at Vieta's formula. So far everything has been straightforward and familiar. Now let us take a look at () from a different point of view. It is known that every real number t, 0 t 1, can be written uniquely in the form 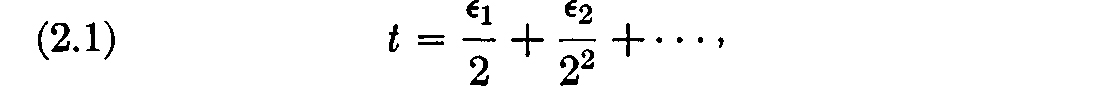 where each is either 0 or 1.
where each is either 0 or 1.
This is the familiar binary expansion of t, and to ensure uniqueness we agree to write terminating expansions in the form in which all digits from a certain point on are 0. Thus, for example, we write 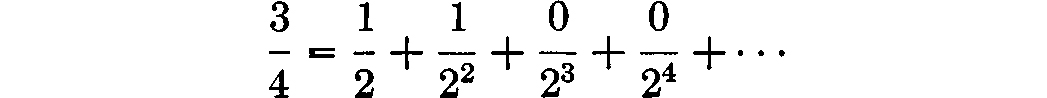 rather than
rather than 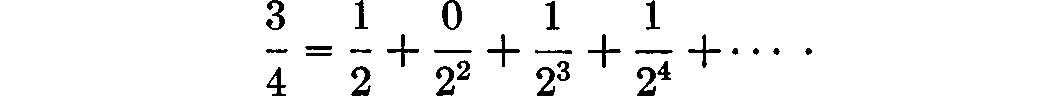 The digits i are, of course, functions of t, and it is more appropriate to write () in the form
The digits i are, of course, functions of t, and it is more appropriate to write () in the form 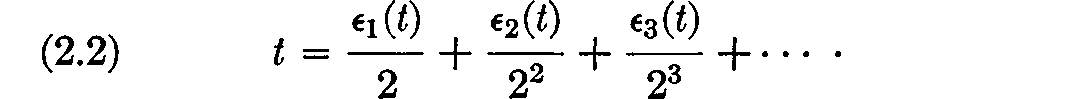 With the convention about terminating expansions, the graphs of 1(t), 2(t), 3(t), are as follows:
With the convention about terminating expansions, the graphs of 1(t), 2(t), 3(t), are as follows: 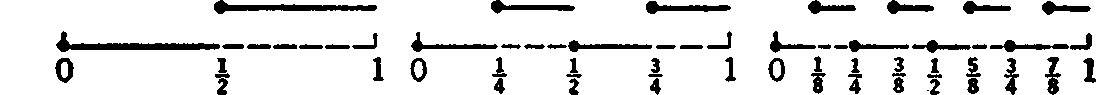 It is more convenient to introduce the functions ri(t) defined by the equations
It is more convenient to introduce the functions ri(t) defined by the equations 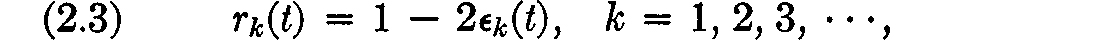 whose graphs look as follows:
whose graphs look as follows:  These functions, first introduced and studied by H. Rademacher, are known as Rademacher functions. In terms of the functions rk(t), we can rewrite () in the form
These functions, first introduced and studied by H. Rademacher, are known as Rademacher functions. In terms of the functions rk(t), we can rewrite () in the form 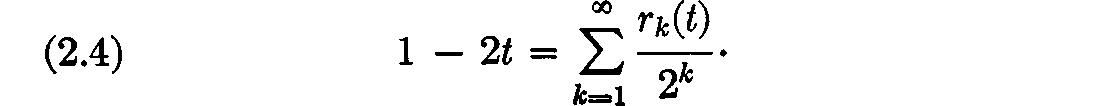
Next page









 Bibliographical Note This Dover edition, first published in 2018, is an unabridged republication of the work originally printed by the Mathematical Association of America, Washington, DC, 1959, as Number 12 in The Carus Mathematical Monographs series. International Standard Book NumberISBN-13: 978-0-486-82158-0ISBN-10: 0-486-82158-7 Manufactured in the United States by LSC Communications 82158701 2018 www.doverpublications.com TO MY TEACHERPROFESSOR HUGO STEINHAUS PREFACE At the meeting of the Mathematical Association of America held in the Summer of 1955, I had the privilege of delivering the Hedrick Lectures. I was highly gratified when, sometime later, Professor T. Rado, on behalf of the Committee on Carus Monographs, kindly invited me to expand my lectures into a monograph. At about the same time I was honored by an invitation from Haverford College to deliver a series of lectures under the Philips Visitors Program. This invitation gave me an opportunity to try out the projected monograph on a "live" audience, and this book is a slightly revised version of my lectures delivered at Haverford College during the Spring Term of 1958.
Bibliographical Note This Dover edition, first published in 2018, is an unabridged republication of the work originally printed by the Mathematical Association of America, Washington, DC, 1959, as Number 12 in The Carus Mathematical Monographs series. International Standard Book NumberISBN-13: 978-0-486-82158-0ISBN-10: 0-486-82158-7 Manufactured in the United States by LSC Communications 82158701 2018 www.doverpublications.com TO MY TEACHERPROFESSOR HUGO STEINHAUS PREFACE At the meeting of the Mathematical Association of America held in the Summer of 1955, I had the privilege of delivering the Hedrick Lectures. I was highly gratified when, sometime later, Professor T. Rado, on behalf of the Committee on Carus Monographs, kindly invited me to expand my lectures into a monograph. At about the same time I was honored by an invitation from Haverford College to deliver a series of lectures under the Philips Visitors Program. This invitation gave me an opportunity to try out the projected monograph on a "live" audience, and this book is a slightly revised version of my lectures delivered at Haverford College during the Spring Term of 1958.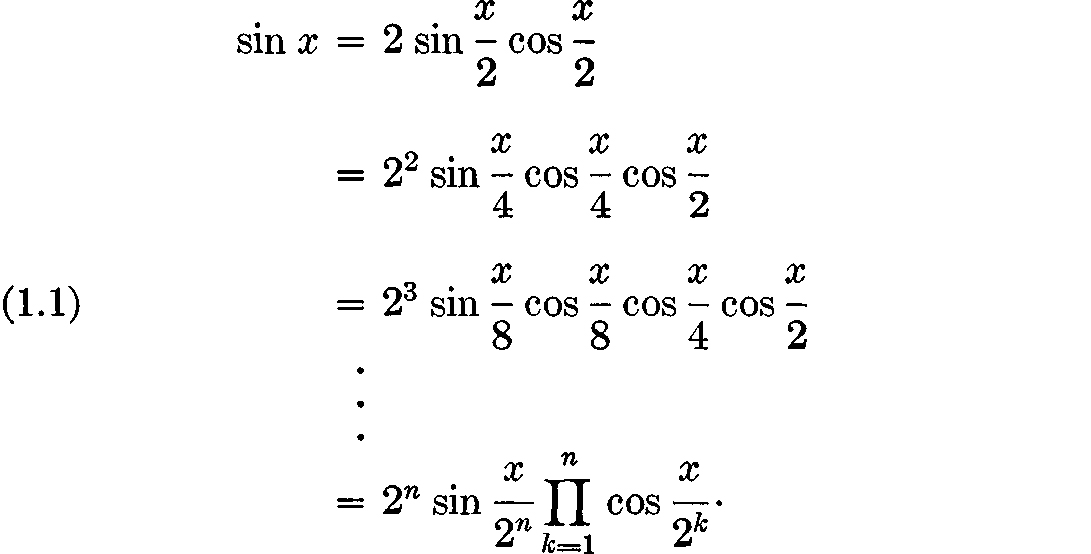 From elementary calculus we know that, for x 0,
From elementary calculus we know that, for x 0, 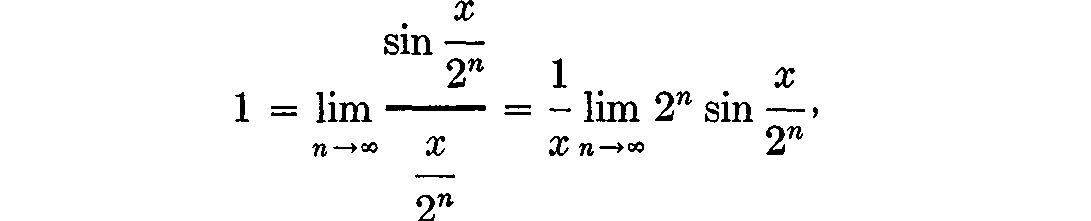 and hence
and hence 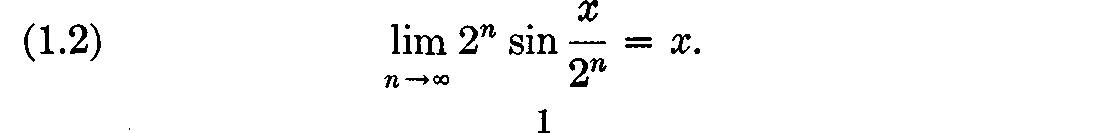 ), we get
), we get 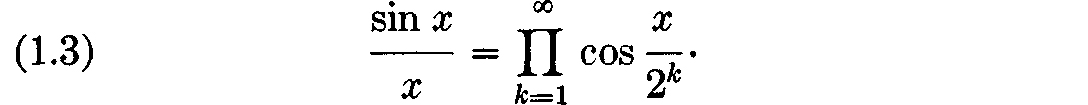 A special case of () is of particular interest. Setting x = /2, we obtain
A special case of () is of particular interest. Setting x = /2, we obtain 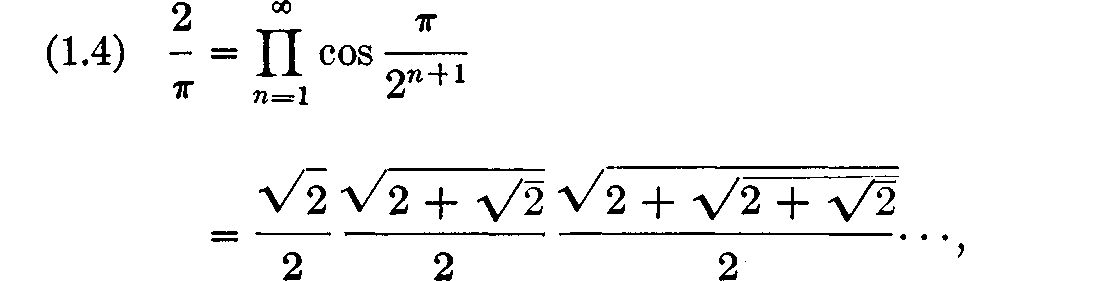 a classical formula due to Vieta. . Another look at Vieta's formula. So far everything has been straightforward and familiar. Now let us take a look at () from a different point of view. It is known that every real number t, 0 t 1, can be written uniquely in the form
a classical formula due to Vieta. . Another look at Vieta's formula. So far everything has been straightforward and familiar. Now let us take a look at () from a different point of view. It is known that every real number t, 0 t 1, can be written uniquely in the form 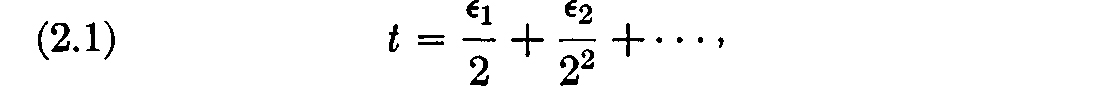 where each is either 0 or 1.
where each is either 0 or 1.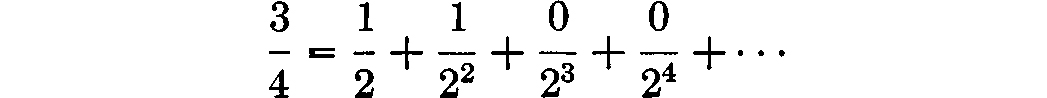 rather than
rather than 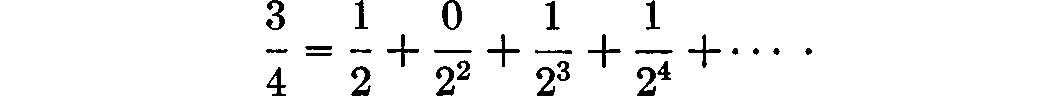 The digits i are, of course, functions of t, and it is more appropriate to write () in the form
The digits i are, of course, functions of t, and it is more appropriate to write () in the form 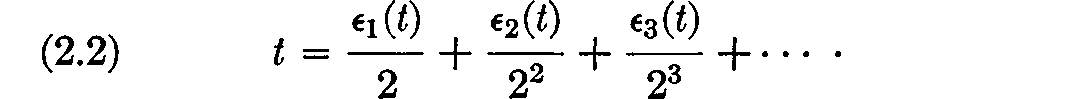 With the convention about terminating expansions, the graphs of 1(t), 2(t), 3(t), are as follows:
With the convention about terminating expansions, the graphs of 1(t), 2(t), 3(t), are as follows: 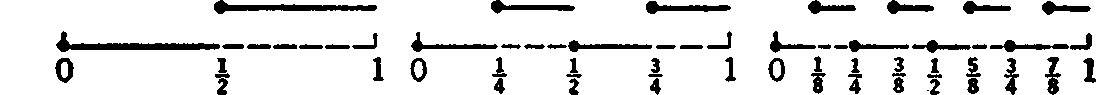 It is more convenient to introduce the functions ri(t) defined by the equations
It is more convenient to introduce the functions ri(t) defined by the equations 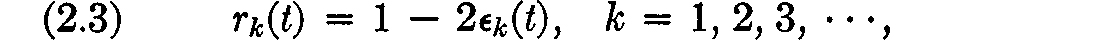 whose graphs look as follows:
whose graphs look as follows:  These functions, first introduced and studied by H. Rademacher, are known as Rademacher functions. In terms of the functions rk(t), we can rewrite () in the form
These functions, first introduced and studied by H. Rademacher, are known as Rademacher functions. In terms of the functions rk(t), we can rewrite () in the form