Answers To Odd-Numbered Problems
SECTION 2.2
{(i, j, k): i, j, k {H, T}}; (iii) Each point of is a subset of 13 cards from {AC, 2C,,KC,,AS, 2S,,KS}; (v) {0, 1,,n}; (vii) {2, 3, 4, 5, 6}; (ix) {(x, y, z): x 1 integral, y > 0, z > 0} (xi) {(x, y): 0 yx 1}; (xiii) {(i, j, k, l, m): i, j, k, l, m
{H, T}}; (iii) Each point of is a subset of 13 cards from {AC, 2C,,KC,,AS, 2S,,KS}; (v) {0, 1,,n}; (vii) {2, 3, 4, 5, 6}; (ix) {(x, y, z): x 1 integral, y > 0, z > 0} (xi) {(x, y): 0 yx 1}; (xiii) {(i, j, k, l, m): i, j, k, l, m {L, R}}.
{L, R}}.
. (i) (a) 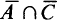 (c) (CA) (AC).
(c) (CA) (AC).
. {(X, y, Z), (X, Z, Y), (Y, X, Z), (Y, Z, X), (Z, X, Y), (Z, Y, X)}; {(X, Y, Z), (X, Z, Y),(Z, X, Y)}; {(X, Y, Z),(X, Z, Y)}; {(Y, X, Z), (Z, X, Y)}.
. (i) {(x, y): 0 xy 1}; (iii) {(x, y): 0 y 3x, 0 x 1, 0 y 1}.
. All subsets of three cities; (i) {{D, P, L}, {D, P, H}, {P, L, H}, {D, L, H}}, etc.
SECTION 2.3
. In parts (ii), (v) and (vii).
. 24/30; 28/30; 28/30.
. 2/10; 7/10; 4/10.
. 6/8.
. 1/9.
. 4/9; 5/9.
SECTION 2.4
. 1/5; 4/5; 12/25; 1/10; 4/125.
..94; .18, .05; .95; .93, .82.
..0106.
. 0.
..45.
..75; .2; .05.
..05; .04; .15; .15; .16; .84; .40; .38; .60.
..75 p .8; .1 p .55; .2 p .25.
SECTION 2.5
. 1680.
. 109 (or 9(10)8 if number cannot begin with zero).
. 4!; 44.
. ll!/(2!)3.
. 45321.
. 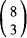 7; 6.
7; 6.
. 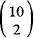 .
.
.  .
.
. 20!/5! 12! 3!.
. 3/103(26)3.
. Yes, P(all men) = 6/143.
. 1/22.
. 1/3; 2/5.
. (1 2/(N 1))2n2.
. 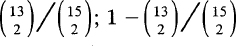 .
.
. Yes, probability 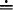 .0151.
.0151.
. 1 999990P3/1000000P3 = .00003.
SECTION 2.6
32/52; 20/52; 22/48.
. 100/126.
. 8/13; .02.
..08.
. 36/91.
. 1/4; 1/3.
..08.
. 173/480; 108/173, 15/173.
..0872.
SECTION 2.7
. (vi).
. Yes.
. 0 or 5/7; .5.
..5 or .2; .2 or .5.
. 1 (1 et0/.
..001; .1; .05; .352; .216.
. 1 (.95)20 (.95)19.
. (i) 16807/279936; (ii) .463, .386, .1285, .0214, .0018, .0001 for j = 1, 2,, 6, etc.
. plp2(2 p1)(2 p2).
SECTION 2.8
. 10p5/105.
. 9; 9.
SECTION 2.9
. Yes in each case.
. (nr + 1)!/n!.
. (1 p)/(2 p); 1/(2 p).
. 1/6; 1/3; 1/3.
. /( + p(1 )).
. 1/18; 1/17.
..90 P(Ai) .95.
. 13/16; 4/13; 12/13.
..00000064; .00043.
. 1 /4; /4; /4; 0.
SECTION 3.2
. 1/2, 1/2; 1/29.
. 16/210, 8/210, 48/210, 48/210.
. (ii) 16/27, 49/81, 5/9.
SECTION 3.3
. No; yes; yes; no.
. P(X = 0) = .18, P(X = 1) = .54, P(X = 2) = .27, P(X = 3) = .02; .82.
. c = 2/15; 1/49; 2/N(N + 1); P(X < 3) = 13/15, 9/49 6/N(N + 1); smallest x = 1, 4, 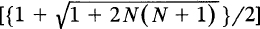 ; largest x = 0, 3,
; largest x = 0, 3, 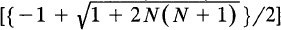 .
.
..8647, .4059, .2706.
. 1 exp{ (x )/} for x ; 1/2 + (arctan x)/.
. Yes; 1/2 for 0 < x < 1, 1/4 for 2 < x < 4; 1/2, |x| ; xex, x < 0; (x l)/4 for 1 x < 3, and P(X = 3) = 1/2; 2xex2, x > 0.
.141; .6988.
..2.
. 20e5, 3/16.
. [e2/ + (1 p)2]/3; 0, e2/[e2/ + (1 p)2]1, (1 p)2[e2/ + (1 p)2]1.
SECTION 3.4
. (ii) 11/36, 13/36.
. (ii) 5/16, 3/8.
. (ii) 23/60, 7/10, 23/60.
. 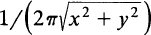 , for |x| 1, |y| 1.
, for |x| 1, |y| 1.
. Yes, 1 e7.
. (iii) 3/4, 9/16.
. 1/24; 15/16.
. f(x, y) = 1, 0 xy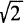 ; 1/4,
; 1/4, 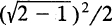
. 1/6, 2/3.
SECTION 3.5
. (ii) X: 64/216, 48/108, 12/54, 1/27; Y:27/216, 27/72, 9/24, 1/8; (iii) P{X = x|Y = y} = 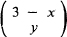 (3/4)y(1/4)3 xy, P{Y = y|X = x} =
(3/4)y(1/4)3 xy, P{Y = y|X = x} = 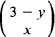 (2/3)x(1/3)3 yx; (iv) 24/47.
(2/3)x(1/3)3 yx; (iv) 24/47.
. X: 9/54, 8/48, 7/42, 6/36, 5/30, 4/24; Y: 1/54, 17/432, 191/3024, 257/3024, 1879/15120, 2509/15120, 2509/15120, 2509/15120, 2509/15120.
. (i) 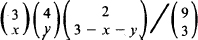 ; (ii)
; (ii) 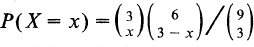 ,
, 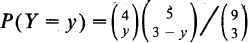 ; (iv) 1/84, 4/84; (v) 1/5, 1/10.
; (iv) 1/84, 4/84; (v) 1/5, 1/10.
. (i) 3x/4 + 5/8; 3/8 + 5y/4; (ii) 105/128, 81/128; (iii) h(y|x) = 2(3x + 5y)/(6x + 5), g(x|y) = 2(3x + 5y)/(3 + 10y).
. f2(y) ln(l y), 0 < y < 1; g(x|y) = 1/[(1 x)ln(l y)], 0 xy; ln(6/5)/ln(8/5).
. 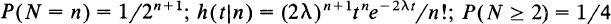 .
.
. 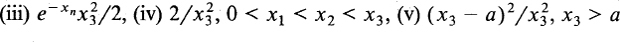 .
.
. f1f2; g(x
Next page










 {H, T}}; (iii) Each point of is a subset of 13 cards from {AC, 2C,,KC,,AS, 2S,,KS}; (v) {0, 1,,n}; (vii) {2, 3, 4, 5, 6}; (ix) {(x, y, z): x 1 integral, y > 0, z > 0} (xi) {(x, y): 0 yx 1}; (xiii) {(i, j, k, l, m): i, j, k, l, m
{H, T}}; (iii) Each point of is a subset of 13 cards from {AC, 2C,,KC,,AS, 2S,,KS}; (v) {0, 1,,n}; (vii) {2, 3, 4, 5, 6}; (ix) {(x, y, z): x 1 integral, y > 0, z > 0} (xi) {(x, y): 0 yx 1}; (xiii) {(i, j, k, l, m): i, j, k, l, m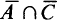 (c) (CA) (AC).
(c) (CA) (AC).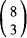 7; 6.
7; 6.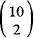 .
. .
.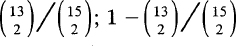 .
.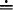 .0151.
.0151.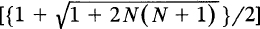 ; largest x = 0, 3,
; largest x = 0, 3, 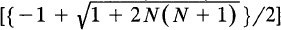 .
.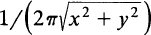 , for |x| 1, |y| 1.
, for |x| 1, |y| 1.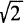 ; 1/4,
; 1/4, 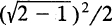
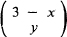 (3/4)y(1/4)3 xy, P{Y = y|X = x} =
(3/4)y(1/4)3 xy, P{Y = y|X = x} = 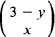 (2/3)x(1/3)3 yx; (iv) 24/47.
(2/3)x(1/3)3 yx; (iv) 24/47.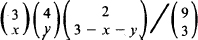 ; (ii)
; (ii) 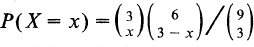 ,
, 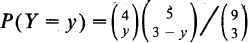 ; (iv) 1/84, 4/84; (v) 1/5, 1/10.
; (iv) 1/84, 4/84; (v) 1/5, 1/10.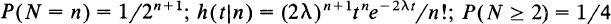 .
.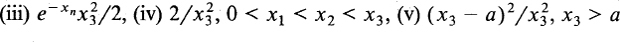 .
.