Bruggemann Rainer - Partial Order Concepts in Applied Sciences
Here you can read online Bruggemann Rainer - Partial Order Concepts in Applied Sciences full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: Cham, year: 2017, publisher: Imprint, Springer, Springer International Publishing, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Partial Order Concepts in Applied Sciences
- Author:
- Publisher:Imprint, Springer, Springer International Publishing
- Genre:
- Year:2017
- City:Cham
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
Partial Order Concepts in Applied Sciences: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Partial Order Concepts in Applied Sciences" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Part I. Theoretical and methodological advances -- 1. Endowing posets with flesh: if, why and how? -- 2. Incomparability/inequality measures and clustering -- 3. Incomparable -- what now, IV. Incomparabilities -- a modeling challenge -- 4. Partial Ordering and Metrology Analyzing Analytical Performance -- 5. Functionals and synthetic indicators over finite posets -- 6. Evaluation, considered as problem orientable mathematics over lattices -- 7.A combined lexicographic-average rank approach for evaluating uncertain multi-indicator matrices with risk metrics -- Part II. Partial Order Theory in socio-economic sciences -- 8. Peculiarities in multidimensional regional poverty -- 9. Application of Partial Order Theory to Multidimensional Poverty Analysis in Switzerland -- 10. Analysis of social participation: a multidimensional approach based on the theory of partial ordering -- 11. POSET analysis of panel data with POSAC -- 12. Partially Ordered Set Theory and Sens capability approach: a fruitful relationship -- Part III. Partial Order Theory in environmental sciences -- 13. Ranking Chemicals with Respect to Accidents Frequency -- 14. Formal Concept Analysis applications in chemistry: from radionuclides and molecular structure to toxicity and diagnosis -- 15. Partial Order Analysis of the government dependence of the Sustainable Development Performance in Germanys Federal States -- Part IV. New applications of Partial Order Theory -- 16.A matching problem, partial order and an analysis applying the Copeland index -- 17. Application of the Mixing Partial Order to Genes -- 18. Analysing ethnopharmacological data matrices on traditional uses of medicinal plants with the contribution of Partial Order Techniques -- Part V. Software developments -- 19. PARSEC: An R package for partial orders in socio-economics -- 20. PyHasse and cloud computing. div>.;This book illustrates recent advances in applications of partial order theory and Hasse diagram techniques to data analysis, mainly in the socio-economic and environmental sciences. For years, partial order theory has been considered a fundamental branch of mathematics of only theoretical interest. In recent years, its effectiveness as a tool for data analysis is increasingly being realized and many applications of partially ordered sets to real problems in statistics and applied sciences have appeared. Main examples pertain to the analysis of complex and multidimensional systems of ordinal data and to problems of multi-criteria decision making, so relevant in social and environmental sciences. Partial Order Concepts in Applied Sciences presents new theoretical and methodological developments in partial order for data analysis, together with a wide range of applications to different topics: multidimensional poverty, economic development, inequality measurement, ecology and pollution, and biology, to mention a few. The book is of interest for applied mathematicians, statisticians, social scientists, environmental scientists and all those aiming at keeping pace with innovation in this interesting, growing and promising research field.
Bruggemann Rainer: author's other books
Who wrote Partial Order Concepts in Applied Sciences? Find out the surname, the name of the author of the book and a list of all author's works by series.
Bruggemann Rainer
Stefani Majer
Jeff D. Colgan
Cleophas Ton J. M.
J. David Logan
David Borthwick
Tai-Ran Hsu
Stanley J. Farlow
Avner Friedman
William George Jacoby
Partial Order Concepts in Applied Sciences — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Partial Order Concepts in Applied Sciences" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Light
Font size:
↓
↑
Reset
Interval:
↓
↑
Bookmark:
Make
Part I
Theoretical and Methodological Advances
Theoretical and Methodological Advances
Springer International Publishing AG 2017
Marco Fattore and Rainer Bruggemann (eds.) Partial Order Concepts in Applied Sciences 10.1007/978-3-319-45421-4_1Endowing Posets with Flesh: If, Why and How?
Jan W. Owsiski 1
(1)
Systems Research Institute, Polish Academy of Science, Newelska 6, 01-447 Warszawa, Poland
Jan W. Owsiski
Email:
Introduction
Resulting from numerous empirical studies are multidimensional data, say x i , i= 1,, n , x i ={ x ik }, with i s denoting observations, or objects, and k =1,, m , denoting the descriptive variables, features, or criteria. We would often like to put these data into a ranking type of a structure, i.e. to order the items i . This means, implicitly, obtaining a sequence of ranks { o i }, corresponding to i =1,, n , where o i are natural numbers ranging from 1 to at most n . (We assume that x ik are the values of measurements regarding certain criteria, numbered k , k K ={1,, m }, and that in all cases the more, the better. None of these assumptions limits the generality of the considerations.) Yet, the sheer multiplicity of dimensions prohibits, as a rule, a straightforward ordering of the data items. This is the obvious consequence of the situations, in which x ik > x jk for some i , j and a definite subset of k K , while x ik < x jk for the same i , j and another subset of k K .
Thus, we very often stop at the result of analysis, being a poset, encompassing all the situations, where x ik x jk for all k K , and leaving out all the other ones, its illustration being constituted by the respective Hasse diagram.
There areindeed numeroussituations, though, in which we would like to go beyond the poset skeleton and endow it with flesh, up to construction of a complete order, perhaps with some additional characterisation. (A feasible alternative might be a kind of information, resulting from the poset processing, that is effectively close enough to the actual ranking.)
We argue here that such extension of a poset may be legitimate, and a shorthand analysis is provided of why and how one could go about it, based on the essential properties of the analytical tasks in general.
Why Not?
There exist serious reservations, concerning going beyond the poset structure as a result of the ordering-oriented study for the given set of data items { x i }.
The primary one is that the empirical data do not contain any other information than that corresponding to the poset obtained. If we go further away from this point, first of all by adding ( i , j ) edges that do not exist on the original Hasse diagram, and especially toward the complete order, then we are unfaithful to the data. There is, actually, an often justified suspicion of manipulation, motivated by political interests, behind the operations, leading from the original data-based poset to some complete order. This suspicion may, of course, be well founded.
The second reservation refers to the fact that while forming a poset from the initial { x i } data is straightforward and unambiguous, virtually all approaches meant to go beyond it either involve subjectivity, or have to refer to data that may have little to do with the original empirical data used in the study.
It is largely in view of these two types of reservations that the technique of counting the consistent linear extensions for a poset is advocated, which, even if still arbitrary, appears to be a possibly neutral operation, based only on the relation between the given poset and the structure of the entire lattice.
But Perhaps
On the other hand, though, there are quite obvious, and, at that, quite numerous and diverse, reasons for insisting on complementing the posets to completeness, or at least somehow transforming it in a definite direction and manner. These result from the considerations, associated with the aspects, roughly illustrated in Fig.. 
Fig. 1
The environment of the studies, leading to data structures, including posets
3.1 The Purpose and the Utility
First is the sheer utility: it may be so that the very objective of the endeavour, from which the data originate, includes the determination of a (possibly) complete order, for quite practical purposes. Lack of such a structure may mean a failure and a loss in economic or social terms.
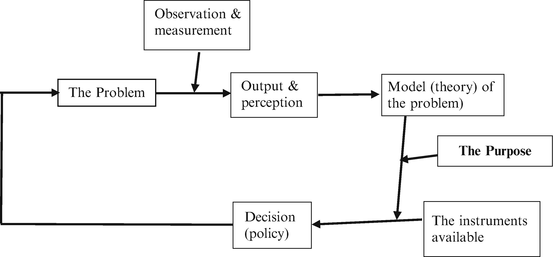
This argument involves a much broader background, involving such notions as: a problem , an image (model, theory, perception) of the problem , the need to deal with it (to resolve it) , the need to cognise it (to identify its structure and mechanism) , the need to apply definite means to resolve the problem , based on the cognition of the problem, on the purpose (the objective ), and the instruments we operate. All these enter the classical decision-making loop of Fig.. 
Fig. 2
The classical decision-making loop, in which the notions referred to appear
If our purpose does not involve (imply) a decision or a policy, an action regarding the problem, then our cognition may be the last step in the procedure, and we might not need anything more than a poset, in case we compare some objects or states, and especially then, when not so much the values x ik are important, as sheer binary relations between them.
This last remark is quite telling. A simplest pertinent situation is outlined in the frame of Example 1 (which will be continued further on, through addition of consecutive aspects).
So, if there is a purpose, requiring action, based on a decision or policy, not only ordering may be required, but also measurement of quantities x i and their transformations (mappings). An illustration of the exposure to a situation with an explicit structure of purpose and instruments is provided below, with a hint to an important proposition.
Assume we deal with two dimensions of wealth: k =1income, and k =2usable wealth, meaning lump assessment of the value of assets, considering mainly their utility and only secondarily their market value (e.g. a car as a transport means, not as a certain saleable good; ownership of a dwelling with its equipment being the primary instance). Even though there is a high correlation between the two dimensions, there are numerous cases when households with lower incomes dispose of an ampler usable wealth. This is especially important when such situations occur close to the border of the derived deprivation function, D (.), namely near D ( x )=0, whether we speak of x .1 or of x .2. If the authorities dispose of only one instrument, the general subsidy , then a single reaction (decision) function S ( D 1, D 2) has to be developed, meaning, in fact, appropriate weighing (implicit or explicit) of the two dimensions. Now, assume that the authorities can deploy a second instrument, say, a non-transferable allowance for housing costs . We deal with S 1( D 1, D 2), S 2( D 1, D 2). The fundamental question is: how are the two pairs of dimensions interrelated? Most conveniently, the dimensions k would correspond directly to the instruments. If such a correspondence existed, even in the form of a demonstrable correlation, then the task of the authorities would be straightforward, and no additional analysis, beyond (two) unidimensional rankings, would be necessary.
Light
Font size:
↓
↑
Reset
Interval:
↓
↑
Bookmark:
Make
Similar books «Partial Order Concepts in Applied Sciences»
Look at similar books to Partial Order Concepts in Applied Sciences. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Stefani Majer
Jeff D. Colgan
Cleophas Ton J. M.
J. David Logan
David Borthwick
Tai-Ran Hsu
Stanley J. Farlow
Avner Friedman
William George Jacoby
Reviews about «Partial Order Concepts in Applied Sciences»
Discussion, reviews of the book Partial Order Concepts in Applied Sciences and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.