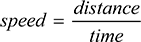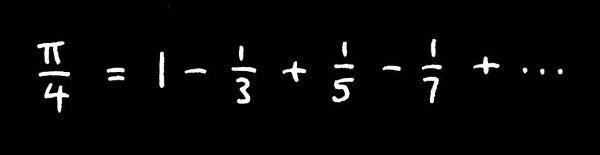David Acheson - The calculus story: a mathematical adventure

Great Clarendon Street, Oxford, OX2 6DP, United Kingdom

Oxford University Press is a department of the University of Oxford. It furthers the Universitys objective of excellence in research, scholarship, and education by publishing worldwide. Oxford is a registered trade mark of Oxford University Press in the UK and in certain other countries

David Acheson 2017

The moral rights of the author have been asserted

First Edition published in 2017

Impression: 1

All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, without the prior permission in writing of Oxford University Press, or as expressly permitted by law, by licence or under terms agreed with the appropriate reprographics rights organization. Enquiries concerning reproduction outside the scope of the above should be sent to the Rights Department, Oxford University Press, at the address above

You must not circulate this work in any other form and you must impose this same condition on any acquirer

Published in the United States of America by Oxford University Press 198 Madison Avenue, New York, NY 10016, United States of America

British Library Cataloguing in Publication Data

Data available

Library of Congress Control Number: 2017935884

ISBN 9780198804543

ebook ISBN 9780192526724

Printed in Great Britain by Clays Ltd, St Ives plc

Links to third party websites are provided by Oxford in good faith and for information only. Oxford disclaims any responsibility for the materials contained in any third party website referenced in this work.

In memory of

Dr Janet Mills

(19542007)

who once claimed that she never quite understood calculus

In the summer of 1666, Isaac Newton saw an apple fall in his garden, and promptly invented the theory of gravity.

That, at least, is the story.

And, however oversimplified this version of events may be, it makes as good a starting point as any for an introduction to calculus.

Because the apple speeds up as it falls.

Newton and the apple.

It even raises the whole question of what we mean, exactly, by the speed of the apple at any given moment.

This is because the well-known formula

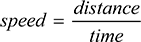
only applies when the speed of motion is constant, i.e. when distance is proportional to time.

To put it another.

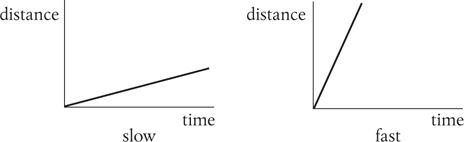
Motion at constant speed.

But, with a falling apple, distance isnt proportional to time. As Galileo discovered, the distance fallen in time t is proportional to t2.

So, after a certain time the apple will have fallen a certain distance, but after twice as long it will have fallen not twice as far but four times as far, because 22 = 4. And if we plot the distance fallen against time we, which bends upwards.

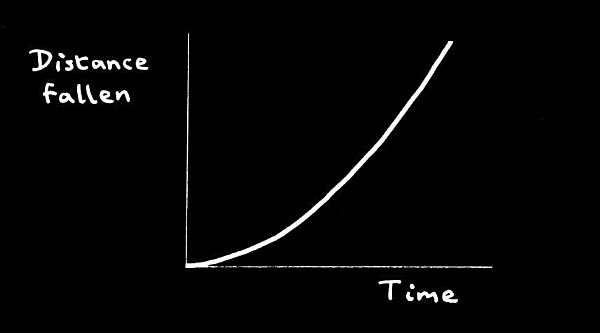
How an apple falls.

Plainly, the increasing steepness of the curve reflects, in some way, the increasing rate at which the apple falls, as time goes on.

And this idea of the rate at which something is changing with time is one of the most central ideas in the whole of calculus.

Calculus is sometimes said to be all about change, but a better description, arguably, is that it is all about the rates at which things change.

(a) Isaac Newton (16421727) (b) Gottfried Leibniz (16461716)

The subject came fully to life in the second half of the 17th century, largely through the work of Isaac Newton, in England, and Gottfried Leibniz, in Germany.

The two never met, but there was a certain amount of wary (and indirect) correspondence between them. At first, this was amicable and polite, but the relationship eventually deteriorated into a major row about who had invented calculus.

While I will say more about this later, my main concern in this short book is with calculus itself.

Above all, I want to offer a big picture of the subject as a whole, concentrating on the most important ideas, and something of their history.

We will see, also, how calculus is fundamental to physics and the other sciences.

).

Guitar string vibrations.

But I will also stress, throughout the book, occasions on which results from calculus can be enjoyed purely for their own sake, regardless of any possible practical application.

, for instance, shows an extraordinary connection between which is all about circlesand the odd numbers.

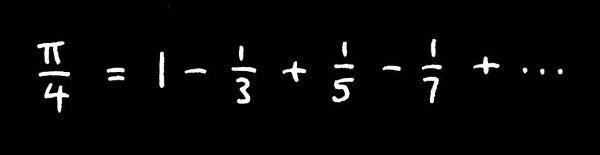
A surprising connection.

And, in due course, I will try to show just why this result is true.

In short, then, this little book is more ambitious than it looks.

If all goes well, we will see not only what calculus is really about, but how to actually start doing it.

And to set about that, we need first to think a little about the very nature and spirit of mathematics itself.

In the Babylonian Collection at Yale University there is a famous clay tablet, known as YBC 7289. It dates from roughly 1700 bc , and has a simple geometrical figure on it ().

Square and diagonals.

The figure is accompanied by some cuneiform writing, and when that was deciphered it was found to be an approximation to the number 2correct to better than 1 part in a million.

How, then, did the writer know that, for a square, the ratio of diagonal to side is 2?

We can only guess, I think, that they appealed to a diagram such as .

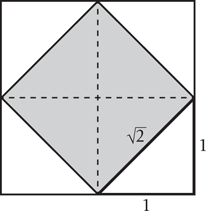
A simple deduction.

The area of the large square is 2 2 = 4. The area of the shaded square is evidently half of this, and therefore 2. So the side of the shaded square must be 2.

Today, this deductive aspect of mathematics is seen as central to the whole subject.