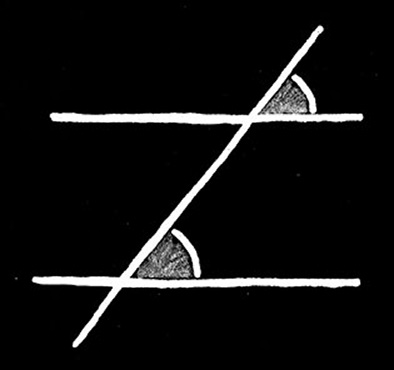David Acheson - The Wonder Book of Geometry: A Mathematical Story

Great Clarendon Street, Oxford, OX2 6DP, United Kingdom

Oxford University Press is a department of the University of Oxford. It furthers the Universitys objective of excellence in research, scholarship, and education by publishing worldwide. Oxford is a registered trade mark of Oxford University Press in the UK and in certain other countries

David Acheson 2020

The moral rights of the author have been asserted

First Edition published in 2020

Impression: 1

All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, without the prior permission in writing of Oxford University Press, or as expressly permitted by law, by licence or under terms agreed with the appropriate reprographics rights organization. Enquiries concerning reproduction outside the scope of the above should be sent to the Rights Department, Oxford University Press, at the address above

You must not circulate this work in any other form and you must impose this same condition on any acquirer

Published in the United States of America by Oxford University Press

198 Madison Avenue, New York, NY 10016, United States of America

British Library Cataloguing in Publication Data

Data available

Library of Congress Control Number: 2020932235

ISBN 9780198846383

ebook ISBN 9780192585387

Printed and bound in Great Britain by

Clays Ltd, Elcograf S.p.A.

Links to third party websites are provided by Oxford in good faith and for information only. Oxford disclaims any responsibility for the materials contained in any third party website referenced in this work.

It all started at school, one cold winter morning in 1956, when I was ten.

Mr. Harding had been doing some maths at the blackboard, with chalk dust raining down everywhere, when he suddenly whirled round and told us all to draw a semicircle, with diameter AB.

Then we had to choose some point P on the semicircle, join it to A and B by straight lines, and measure the angle at P ().

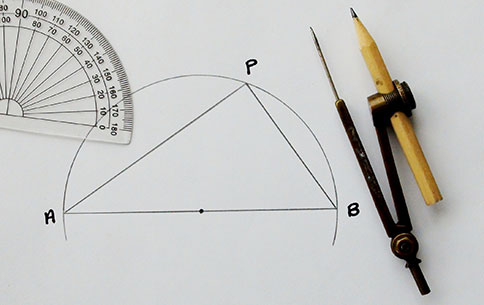
Fig. 1 Thales theorem.

I duly got on with all this, casually assuming that the angle at P would depend on where P is, exactly, on the semicircle.

But it doesnt.

Its always 90.

* * *

At the time, I had no idea that mathematics is full of surprises like this.

I had no idea, either, that this is one of the first great theorems of geometry, due to a mathematician called Thales, in ancient Greece. And according to Thales so it is said the key question is always not What do we know? but rather How do we know it?

Why is it, then, that the angle in a semicircle is always 90?

The short answer is that we can prove it, by a sequence of simple logical steps, from a few apparently obvious starting assumptions.

Fig. 2 The importance of proof.

And by doing just that, in the next few pages, I hope to not only lay some foundations for geometry, but do something far more ambitious.

For, with geometry, it is possible to see something of the whole nature and spirit of mathematics at its best, at almost any age, within just half an hour of starting.

And in case you dont quite believe me

The first really major idea is that of parallel lines.

These are lines, in the same plane, which never meet, no matter how far they are extended.

And I will make two assumptions about them.

Parallel lines

Imagine, if you will, two lines crossed by a third line, producing the so-called corresponding angles of .

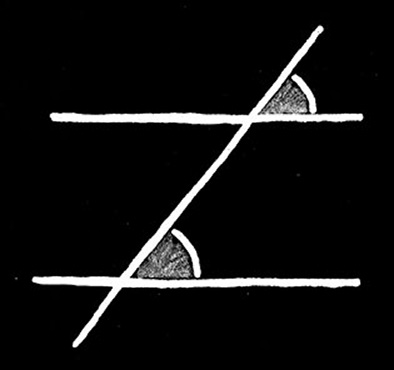
Fig. 3 Corresponding angles.

Then, throughout most of this book, I will assume that

(1) If two lines are parallel, the corresponding angles are equal.

(2) If corresponding angles are equal, the two lines are parallel.

These assumptions are rooted in the intuitive notion that parallel lines must be, so to speak, in the same direction, but however obvious (1) and (2) may seem, they are assumptions.

And, even at this early stage, it is worth noting that they amount to two very different statements.

In effect, (1) helps us use parallel lines, while (2) helps us show that we have some.

Angles

We will measure angles in degrees, denoted by , and the two parts of a straight line through some point P form an angle of 180 ().

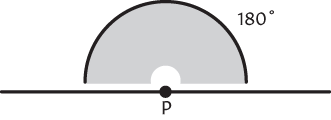
Fig. 4 A straight line.

A right angle is half this, i.e. an angle of 90, and the two lines forming it are then said to be perpendicular ().

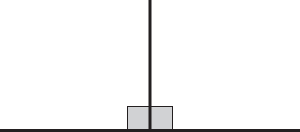
Fig. 5 Right angles.

Opposite angles

When two straight lines intersect, the so-called opposite angles are equal ().

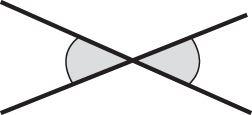
Fig. 6 Opposite angles.

Alternate angles

If two lines are parallel, and crossed by a third line, then the so-called alternate angles are equal ().

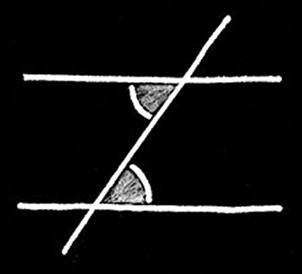
Fig. 7 Alternate angles.

This is because, in , a = b (corresponding angles) and b = c (opposite angles). So a = c.

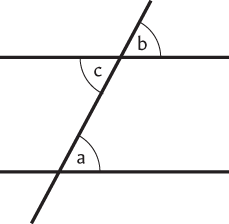
Fig. 8 Proof that alternate angles are equal.

The argument works in reverse, too, so that if alternate angles are equal, the two lines must be parallel.

And with these ideas in place, we are now ready to prove the first theorem which, in my view, is not obvious at all

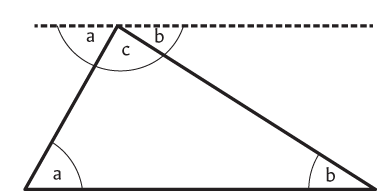
The angle-sum of a triangle

The three angles in any triangle add up to 180 ().

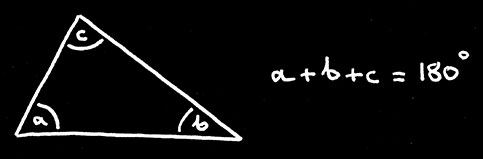
Fig. 9 Angles in a triangle.

To prove this, draw a straight line through one corner, parallel to the opposite side ().