Francesco Catoni , Dino Boccaletti , Roberto Cannata , Vincenzo Catoni and Paolo Zampetti SpringerBriefs in Physics Geometry of Minkowski Space-Time 10.1007/978-3-642-17977-8_1 Francesco Catoni 2011
1. Introduction
Francesco Catoni 1
(1)
ENEA, Via Veglia 10, 00141 Rome, Italy
(2)
Department of Mathematics, University of Rome La Sapienza, Piazzale Aldo Moro 2, 00185 Rome, Italy
(3)
Casaccia Research Centre, ENEA, Via Anguillarese 301, 00123 Rome, Italy
Francesco Catoni (Corresponding author)
Email:
Abstract
It is largely known that the Theory of Special Relativity was born as a consequence of the demonstrated impossibility for the Maxwells electromagnetic (e.m.) theory of obeying Galilean transformations. The non-invariance of the e.m. theory under Galilean transformations induced the theoretical physicists, at the end of the twelfth century, to invent new spacetime transformations which did not allow to consider the time variable as absolutely independent of the space coordinates. It was thus that the transformations which, for the sake of brevity, today we call Lorentz transformations were born.
It is largely known that the Theory of Special Relativity was born as a consequence of the demonstrated impossibility for the Maxwells electromagnetic (e.m.) theory of obeying Galilean transformations. The non-invariance of the e.m. theory under Galilean transformations induced the theoretical physicists, at the end of the twelfth century, to invent new spacetime transformations which did not allow to consider the time variable as absolutely independent of the space coordinates. It was thus that the transformations which, for the sake of brevity, today we call Lorentz transformations were born.
A consequence of the choice of the Lorentz transformations as the ones which keep the e. m. theory invariant when passing from an inertial system to another one (e.g. the e.m. waves remain e.m. waves) was to revolutionize the kinematics, i.e. the basis from which one must start for building the mechanics. It was no longer possible, at least for high velocities, to use Galilean transformations: when passing from an inertial system to another one, also the time variable (until when considered as the independent variable) was forced to be transformed together with the space coordinates.
After the works of Lorentz and Poincar, it was Einsteins turn to build a relativistic mechanics starting from the kinematics based on Lorentz transformations.
However, we owe to Hermann Minkowski the creation of a four-dimensional geometry in which the time entered as the fourth coordinate: the Minkowski spacetime as it is called today.
We recall that for a long period of time the introduction of i t (where i is the imaginary unit) as the fourth coordinate was into use with the aim of providing to spacetime a pseudo-Euclidean structure.
We shall see in this book that it is not the introduction of an imaginary time, but of a system of numbers (the hyperbolic numbers) related in many respects with complex numbers, that can describe the relation (symmetry) between space and time. Moreover this system of numbers allows one a mathematical formalization that, from a logical point of view (an axiomaticdeductive method starting from axioms of empirical evidence) as well as from a practical one (the problems are solved in the same automatic way as the problems of analytical geometry and trigonometry are), is equivalent to the analytical formalization of Euclidean geometry.
Even though Minkowski already introduced hyperbolas in place of calibration circles and a copious literature on the subject does exist, until now a formalization, rigorous and extremely simple at the same time, was not obtained.
In this book we explain how to treat any problem of relativistic kinematics. The expounded formalization allows one to reach an exhaustive and non-ambiguous solution.
The final appendix, while contains a short outline on the evolution of the concept of geometry, helps us to reflect upon the nature of the operation made by the authors: a Euclidean way for facing a non-Euclidean geometry.
Footnotes
An exhaustive account of the subject and its historical context can be found in the bookArthur I. Miller: Albert Einsteins Special Theory of RelativitySpringer, 1998
Francesco Catoni , Dino Boccaletti , Roberto Cannata , Vincenzo Catoni and Paolo Zampetti SpringerBriefs in Physics Geometry of Minkowski Space-Time 10.1007/978-3-642-17977-8_2 Francesco Catoni 2011
2. Hyperbolic Numbers
Francesco Catoni 1
(1)
ENEA, Via Veglia 10, 00141 Rome, Italy
(2)
Department of Mathematics, University of Rome La Sapienza, Piazzale Aldo Moro 2, 00185 Rome, Italy
(3)
Casaccia Research Centre, ENEA, Via Anguillarese 301, 00123 Rome, Italy
Francesco Catoni (Corresponding author)
Email:
Abstract
Complex numbers can be considered as a two components quantity, as the plane vectors. Following Gauss complex numbers are also used for representing vectors in Euclidean plane. As a difference with vectors the multiplication of two complex numbers is yet a complex number. By means of this property complex numbers can be generalized and hyperbolic numbers that have properties corresponding to Lorentz group of two-dimensional Special Relativity are introduced.
Keywords
Complex numbers Gauss-Argand Generalization of complex numbers Hyperbolic numbers Space-time geometry Lorentz group
Complex numbers represent one of the most intriguing and emblematic discoveries in the history of science. Even if they were introduced for an important but restricted mathematical purpose, they came into prominence in many branches of mathematics and applied sciences. This association with applied sciences generated a synergistic effect: applied sciences gave relevance to complex numbers and complex numbers allowed formalizing practical problems. A similar effect can be found today in the system of hyperbolic numbers, which has acquired the meaning and importance as the Mathematics of Special Relativity , as shown in this book.
Let us recall some points from the history of complex numbers and their generalization.
Complex numbers are today introduced with the purpose of extending the field of real numbers and for having always two solutions for the second degree equations and, as an important applicative example, we recall the Gauss Fundamental theorem of algebra stating that all the algebraic equations of degree
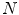
has
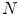
real or imaginary roots. Further Gauss has shown that complex and real numbers are adequate for obtaining all the solutions for any degree equation.
Coming back to complex numbers we now recall how their introduction has a practical reason. Actually they were introduced in the 16th century for solving a mathematical paradox: to give a sense to the real solutions of cubic equations that appear as the sum of square roots of negative quantities (see ). Really the goal of mathematical equations was to solve practical problems, in particular geometrical problems, and if the solutions were square roots of negative quantities, as can happen for the second degree equations, it simply meant that the problem does not have solutions. Therefore it was unexplainable that the real solutions of a problem were given by some imaginary quantities as the square roots of negative numbers.
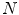 has
has 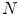 real or imaginary roots. Further Gauss has shown that complex and real numbers are adequate for obtaining all the solutions for any degree equation.
real or imaginary roots. Further Gauss has shown that complex and real numbers are adequate for obtaining all the solutions for any degree equation.










