
 Copyright 2013 by The McGraw-Hill Companies, Inc. All rights reserved. Except as permitted under the United States Copyright Act of 1976, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without the prior written permission of the publisher. ISBN 978-0-07-179560-9
Copyright 2013 by The McGraw-Hill Companies, Inc. All rights reserved. Except as permitted under the United States Copyright Act of 1976, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without the prior written permission of the publisher. ISBN 978-0-07-179560-9
MHID 0-07-179560-X The material in this eBook also appears in the print version of this title: ISBN 978-0-07-179559-3, MHID 0-07-179559-6. All trademarks are trademarks of their respective owners. Rather than put a trademark symbol after every occurrence of a trademarked name, we use names in an editorial fashion only, and to the benefit of the trademark owner, with no intention of infringement of the trademark.
Where such designations appear in this book, they have been printed with initial caps. McGraw-Hill eBooks are available at special quantity discounts to use as premiums and sales promotions, or for use in corporate training programs. To contact a representative please e-mail us at bulksales@mcgraw-hill.com. TERMS OF USE This is a copyrighted work and The McGraw-Hill Companies, Inc. (McGraw-Hill) and its licensors reserve all rights in and to the work. Use of this work is subject to these terms.
Except as permitted under the Copyright Act of 1976 and the right to store and retrieve one copy of the work, you may not decompile, disassemble, reverse engineer, reproduce, modify, create derivative works based upon, transmit, distribute, disseminate, sell, publish or sublicense the work or any part of it without McGraw-Hills prior consent. You may use the work for your own noncommercial and personal use; any other use of the work is strictly prohibited. Your right to use the work may be terminated if you fail to comply with these terms. THE WORK IS PROVIDED AS IS. McGRAW-HILL AND ITS LICENSORS MAKE NO GUARANTEES OR WARRANTIES AS TO THE ACCURACY, ADEQUACY OR COMPLETENESS OF OR RESULTS TO BE OBTAINED FROM USING THE WORK, INCLUDING ANY INFORMATION THAT CAN BE ACCESSED THROUGH THE WORK VIA HYPERLINK OR OTHERWISE, AND EXPRESSLY DISCLAIM ANY WARRANTY, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO IMPLIED WARRANTIES OF MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE. McGraw-Hill and its licensors do not warrant or guarantee that the functions contained in the work will meet your requirements or that its operation will be uninterrupted or error free.
Neither McGraw-Hill nor its licensors shall be liable to you or anyone else for any inaccuracy, error or omission, regardless of cause, in the work or for any damages resulting therefrom. McGraw-Hill has no responsibility for the content of any information accessed through the work. Under no circumstances shall McGraw-Hill and/or its licensors be liable for any indirect, incidental, special, punitive, consequential or similar damages that result from the use of or inability to use the work, even if any of them has been advised of the possibility of such damages. This limitation of liability shall apply to any claim or cause whatsoever whether such claim or cause arises in contract, tort or otherwise.
Preface to the
Second Edition
This edition has been expanded by material on average rate of change, price/demand, polar form of complex numbers, conic sections in polar coordinates, and the algebra of the dot product. An entire chapter () is included as an introduction to differential calculus, which now appears in many precalculus texts.
More than 30 solved and more than 110 supplementary problems have been added. Thanks are due to Anya Kozorez and her staff at McGraw-Hill, and to Madhu Bhardwaj and her staff at International Typesetting and Composition. Also, the author would like to thank the users who sent him (mercifully few) corrections, in particular D. Mehaffey and B. DeRoes. Most of all he owes thanks once again to his wife Gitta, whose careful checking eliminated numerous errors.
Any further errors that users spot would be gratefully received at fsafier@ccsf.edu or fsafier@ccsf.cc.ca.us. Fred Safier
Preface to the
First Edition
A course in precalculus is designed to prepare college students for the level of algebraic skills and knowledge that is expected in a calculus class. Such courses, standard at two-year and four-year colleges, review the material of algebra and trigonometry, emphasizing those topics with which familiarity is assumed in calculus. Key unifying concepts are those of functions and their graphs. The present book is designed as a supplement to college courses in precalculus. The material is divided into forty-four chapters, and covers basic algebraic operations, equations, and inequalities, functions and graphs, and standard elementary functions including polynomial, rational, exponential, and logarithmic functions.
Trigonometry is covered in , and the emphasis is on trigonometric functions as defined in terms of the unit circle. The course concludes with matrices, determinants, systems of equations, analytic geometry of conic sections, and discrete mathematics. Each chapter starts with a summary of the basic definitions, principles, and theorems, accompanied by elementary examples. The heart of the chapter consists of solved problems, which present the material in logical order and take the student through the development of the subject. The chapter concludes with supplementary problems with answers. These provide drill on the material and develop some ideas further.
The author would like to thank his friends and colleagues, especially F. Cerrato, G. Ling, and J. Morell, for useful discussions. Thanks are also due to the staff of McGraw-Hill and to the reviewer of the text for their invaluable help. Most of all he owes thanks to his wife Gitta, whose careful line-by-line checking of the manuscript eliminated numerous errors.
Any errors that remain are entirely his responsibility, and students and teachers who find errors are invited to send him email at fsafier@ccsf.cc.ca.us.
Contents
CHAPTER 1
Preliminaries
The Sets of Numbers Used in Algebra
The sets of numbers used in algebra are, in general, subsets of
R, the set of real numbers.
Natural NumbersN The counting numbers, e.g., 1, 2, 3, 4,
IntegersZ The counting numbers, together with their opposites and 0, e.g., 0, 1, 2, 3, 1, 2, 3,
Rational NumbersQ The set of all numbers that can be written as quotients
a/
b,
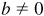
,
a and
b integers, e.g., 3/17, 10/3, -5.13,
Irrational NumbersH All real numbers that are not rational numbers, e.g., ,
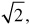
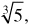
-/3,
EXAMPLE 1.1 The number 5 is a member of the sets
Z, Q,R. The number 156.73 is a member of the sets
Q,R. The number 5 is a member of the sets
H,R.
Axioms for the Real Number System
There are two fundamental operations, addition and multiplication, that have the following properties (
Next page




 Copyright 2013 by The McGraw-Hill Companies, Inc. All rights reserved. Except as permitted under the United States Copyright Act of 1976, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without the prior written permission of the publisher. ISBN 978-0-07-179560-9
Copyright 2013 by The McGraw-Hill Companies, Inc. All rights reserved. Except as permitted under the United States Copyright Act of 1976, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without the prior written permission of the publisher. ISBN 978-0-07-179560-9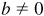 , a and b integers, e.g., 3/17, 10/3, -5.13, Irrational NumbersH
, a and b integers, e.g., 3/17, 10/3, -5.13, Irrational NumbersH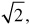
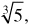 -/3, EXAMPLE 1.1 The number 5 is a member of the sets Z, Q,R. The number 156.73 is a member of the sets Q,R. The number 5 is a member of the sets H,R.
-/3, EXAMPLE 1.1 The number 5 is a member of the sets Z, Q,R. The number 156.73 is a member of the sets Q,R. The number 5 is a member of the sets H,R.