CHAPTER 33
Eigenfunction Expansions
PIECEWISE SMOOTH FUNCTIONS
A wide class of functions can be represented by infinite series of eigenfunctions of a SturmLiouville problem (see ).
Definition: A function
f(
x) is
piecewise continuous on the open interval a <
x <
b if (1)
f(
x) is continuous everywhere in
a <
x <
b with the possible exception of at most a
finite number of points
x,
x, ,
x n and (2) at these points of discontinuity, the right- and left-hand limits of
f(
x), respectively lim
f(
x) and lim
f(
x), exist (
j = 1, 2,...,
n).

(Note that a continuous function is piecewise continuous.)
Definition: A function
f(
x) is
piecewise continuous on the closed interval axb if (1) it is piecewise continuous on the open interval
a <
x <
b, (2) the right-hand limit of
f(
x) exists at
x =
a, and (3) the left-hand limit of
f(
x) exists at
x =
b.
Definition: A function
f(
x) is
piecewise smooth on [
a,
b] if both
f(
x) and
f(
x) are piecewise continuous on [
a,
b].
Theorem 33.1. If
f(
x) is piecewise smooth on [
a,
b] and if {
e n (
x)} is the set of all eigenfunctions of a SturmLiouville problem (see Property 32.3), then

where

The representation (
33.1) is valid at all points in the open interval (
a,
b) where
f(
x) is continuous. (
32.6). (
32.6).
Because different SturmLiouville problems usually generate different sets of eigenfunctions, a given piecewise smooth function will have many expansions of the form (33.1). The basic features of all such expansions are exhibited by the trigonometric series discussed below.
FOURIER SINE SERIES
The eigenfunctions of the SturmLiouville problem
y" +
y = 0;
y(0) = 0,
y(
L) = 0, where
L is a real positive number, are
e n (
x) = sin (
nx/
L) (
n = 1, 2, 3, ). Substituting these functions into (
33.1), we obtain

For this SturmLiouville problem,
w(
x) 1,
a = 0, and
b =
L; so that
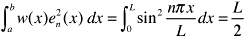
and
(33.2) becomes

The expansion (
33.3) with coefficients given by (
33.4) is the
Fourier sine series for
f(
x) on (0,
L).
FOURIER COSINE SERIES
The eigenfunctions of the SturmLiouville problem
y" +
y = 0;
y(0) = 0,
y(
L) = 0, where
L is a real positive number, are
e(
x) = 1 and
e n (
x) = cos (
nx/
L) (
n = 1, 2, 3, ). Here = 0 is an eigenvalue with corresponding eigenfunction
e(
x) = 1.
Substituting these functions into (33.1), where because of the additional eigenfunction e(x) the summation now begins at n = 0, we obtain  For this SturmLiouville problem, w(x) 1, a = 0, and b = L; so that
For this SturmLiouville problem, w(x) 1, a = 0, and b = L; so that 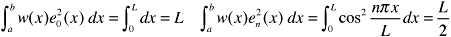 Thus (33.2) becomes
Thus (33.2) becomes 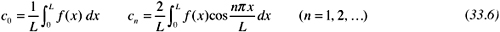 The expansion (33.5) with coefficients given by (33.6) is the Fourier cosine series for f(x) on (0, L).
The expansion (33.5) with coefficients given by (33.6) is the Fourier cosine series for f(x) on (0, L).
Solved Problems
33.1. Determine whether
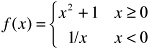
is piecewise continuous on [1, 1]. The given function is continuous everywhere on [1, 1] except at
x = 0. Therefore, if the right- and left-hand limits exist at
x = 0,
f(
x) will be piecewise continuous on [1, 1]. We have
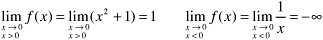
Since the left-hand limit does not exist,
f(
x) is not piecewise continuous on [1, 1]. (Note that
f(
x) is continuous at
x = 1.) At the two points of discontinuity, we find that
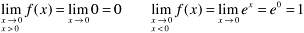
and

Since all required limits exist,
f(
x) is piecewise continuous on [2, 5].
33.3. Is the function
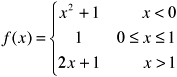
piecewise smooth on [2, 2]? The function is continuous everywhere on [2, 2] except at
x = 1.
33.3. Is the function
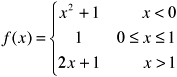
piecewise smooth on [2, 2]? The function is continuous everywhere on [2, 2] except at
x = 1.
Since the required limits exist at x, f(x) is piecewise continuous. Differentiating f(x), we obtain 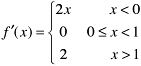 The derivative does not exist at x = 1 but is continuous at all other points in [2, 2]. At x the required limits exist; hence f(x) is piecewise continuous. It follows that f(x) is piecewise smooth on [2, 2]. 33.4. Is the function
The derivative does not exist at x = 1 but is continuous at all other points in [2, 2]. At x the required limits exist; hence f(x) is piecewise continuous. It follows that f(x) is piecewise smooth on [2, 2]. 33.4. Is the function 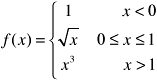 piecewise smooth on [1, 3]? The function f(x) is continuous everywhere on [1, 3] except at x = 0. Since the required limits exist at
piecewise smooth on [1, 3]? The function f(x) is continuous everywhere on [1, 3] except at x = 0. Since the required limits exist at




 (Note that a continuous function is piecewise continuous.) Definition: A function f(x) is piecewise continuous on the closed interval axb if (1) it is piecewise continuous on the open interval a <x <b, (2) the right-hand limit of f(x) exists at x = a, and (3) the left-hand limit of f(x) exists at x = b. Definition: A function f(x) is piecewise smooth on [a, b] if both f(x) and f(x) are piecewise continuous on [a, b]. Theorem 33.1. If f(x) is piecewise smooth on [a, b] and if {e n (x)} is the set of all eigenfunctions of a SturmLiouville problem (see Property 32.3), then
(Note that a continuous function is piecewise continuous.) Definition: A function f(x) is piecewise continuous on the closed interval axb if (1) it is piecewise continuous on the open interval a <x <b, (2) the right-hand limit of f(x) exists at x = a, and (3) the left-hand limit of f(x) exists at x = b. Definition: A function f(x) is piecewise smooth on [a, b] if both f(x) and f(x) are piecewise continuous on [a, b]. Theorem 33.1. If f(x) is piecewise smooth on [a, b] and if {e n (x)} is the set of all eigenfunctions of a SturmLiouville problem (see Property 32.3), then  where
where  The representation (33.1) is valid at all points in the open interval (a, b) where f(x) is continuous. (32.6). (32.6).
The representation (33.1) is valid at all points in the open interval (a, b) where f(x) is continuous. (32.6). (32.6).  For this SturmLiouville problem, w(x) 1, a = 0, and b = L; so that
For this SturmLiouville problem, w(x) 1, a = 0, and b = L; so that 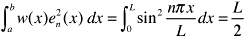 and (33.2) becomes
and (33.2) becomes  The expansion (33.3) with coefficients given by (33.4) is the Fourier sine series for f(x) on (0, L).
The expansion (33.3) with coefficients given by (33.4) is the Fourier sine series for f(x) on (0, L).  For this SturmLiouville problem, w(x) 1, a = 0, and b = L; so that
For this SturmLiouville problem, w(x) 1, a = 0, and b = L; so that 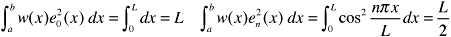 Thus (33.2) becomes
Thus (33.2) becomes 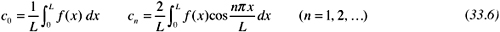 The expansion (33.5) with coefficients given by (33.6) is the Fourier cosine series for f(x) on (0, L).
The expansion (33.5) with coefficients given by (33.6) is the Fourier cosine series for f(x) on (0, L).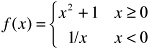 is piecewise continuous on [1, 1]. The given function is continuous everywhere on [1, 1] except at x = 0. Therefore, if the right- and left-hand limits exist at x = 0, f(x) will be piecewise continuous on [1, 1]. We have
is piecewise continuous on [1, 1]. The given function is continuous everywhere on [1, 1] except at x = 0. Therefore, if the right- and left-hand limits exist at x = 0, f(x) will be piecewise continuous on [1, 1]. We have 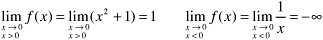 Since the left-hand limit does not exist, f(x) is not piecewise continuous on [1, 1]. (Note that f(x) is continuous at x = 1.) At the two points of discontinuity, we find that
Since the left-hand limit does not exist, f(x) is not piecewise continuous on [1, 1]. (Note that f(x) is continuous at x = 1.) At the two points of discontinuity, we find that 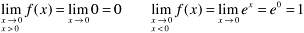 and
and  Since all required limits exist, f(x) is piecewise continuous on [2, 5]. 33.3. Is the function
Since all required limits exist, f(x) is piecewise continuous on [2, 5]. 33.3. Is the function 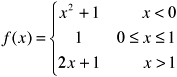 piecewise smooth on [2, 2]? The function is continuous everywhere on [2, 2] except at x = 1. 33.3. Is the function
piecewise smooth on [2, 2]? The function is continuous everywhere on [2, 2] except at x = 1. 33.3. Is the function 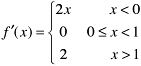 The derivative does not exist at x = 1 but is continuous at all other points in [2, 2]. At x the required limits exist; hence f(x) is piecewise continuous. It follows that f(x) is piecewise smooth on [2, 2]. 33.4. Is the function
The derivative does not exist at x = 1 but is continuous at all other points in [2, 2]. At x the required limits exist; hence f(x) is piecewise continuous. It follows that f(x) is piecewise smooth on [2, 2]. 33.4. Is the function 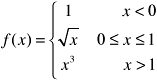 piecewise smooth on [1, 3]? The function f(x) is continuous everywhere on [1, 3] except at x = 0. Since the required limits exist at
piecewise smooth on [1, 3]? The function f(x) is continuous everywhere on [1, 3] except at x = 0. Since the required limits exist at