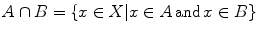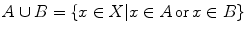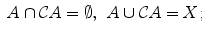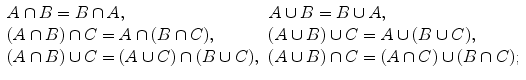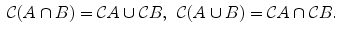In this introductory chapter some mathematical notions are presented rapidly, which lie at the heart of the study of Mathematical Analysis. Most should already be known to the reader, perhaps in a more thorough form than in the following presentation. Other concepts may be completely new, instead. The treatise aims at fixing much of the notation and mathematical symbols frequently used in the sequel.
1.1 1.1 Sets
We shall denote sets mainly by upper case letters X, Y ,, while for the members or elements of a set lower case letters x, y , will be used. When an element x is in the set X one writes x X ( x is an element of X , or the element x belongs to the set X ), otherwise the symbol x X is used.
The majority of sets we shall consider are built starting from sets of numbers. Due to their importance, the main sets of numbers deserve special symbols, namely:
The definition and main properties of these sets, apart from the last one, will be briefly recalled in .
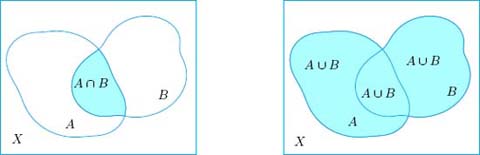
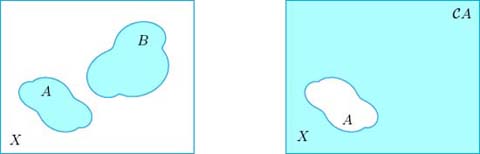
Let us fix a non-empty set X , considered as ambient set . A subset A of X is a set all of whose elements belong to X ; one writes A X ( A is contained, or included, in X ) if the subset A is allowed to possibly coincide with X , and A X ( A is properly contained in X ) in case A is a proper subset of X , that is, if it does not exhaust the whole X . Prom the intuitive point of view it may be useful to represent subsets as bounded regions in the plane using the so-called Venn diagrams (see , left).
Figure 1.1.
Venn diagrams (left) and complement (right)
A subset can be described by listing the elements of X which belong to it
the order in which elements appear is not essential. This clearly restricts the use of such notation to subsets with few elements. More often the notation
will be used (read A is the subset of elements x of X such that the condition p ( x ) holds); p ( x ) denotes the characteristic property of the elements of the subset, i.e., the condition that is valid for the elements of the subset only, and not for other elements. For example, the subset A of natural numbers smaller or equal than 4 may be denoted
The expression p ( x ) = x 4 is an example of predicate , which we will return to in the following section.
The collection of all subsets of a given set X forms the power set of X , and is denoted by
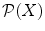
. Obviously
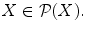
. Among the subsets of X there is the empty set , the set containing no elements. It is usually denoted by the symbol , so
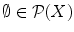
. All other subsets of X are proper and non-empty.
Consider for instance X = {1, 2, 3} as ambient set. Then
Note that X contains 3 elements (it has cardinality 3), while
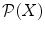
has 8 = 23 elements, hence has cardinality 8. In general if a finite set (a set with a finite number of elements) has cardinality n , the power set of X has cardinality 2 n .
Starting from one or more subsets of X , one can define new subsets by means of set-theoretical operations. The simplest operation consists in taking the complement: if A is a subset of X , one defines the complement of A (in X ) to be the subset
made of all elements of X not belonging to A (, right).
Sometimes, in order to underline that complements are taken with respect to the ambient space X , one uses the more precise notation
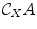
. The following properties are immediate:
For example, if X = and A is the subset of even numbers (multiples of 2), then
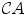
is the subset of odd numbers.
Given two subsets A and B of X , one defines intersection of A and B the subset
containing the elements of X that belong to both A and B , and union of A and B the subset
made of the elements that are either in A or in B (this is meant non-exclusively, so it includes elements of A B ), see .
Figure 1.2.
Intersection and union of sets
We recall some properties of these operations.
ii)
commutative, associative and distributive properties :














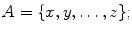
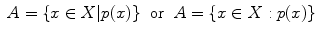
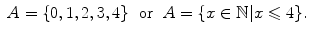
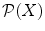 . Obviously
. Obviously 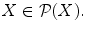 . Among the subsets of X there is the empty set , the set containing no elements. It is usually denoted by the symbol , so
. Among the subsets of X there is the empty set , the set containing no elements. It is usually denoted by the symbol , so 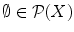 . All other subsets of X are proper and non-empty.
. All other subsets of X are proper and non-empty.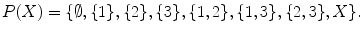
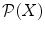 has 8 = 23 elements, hence has cardinality 8. In general if a finite set (a set with a finite number of elements) has cardinality n , the power set of X has cardinality 2 n .
has 8 = 23 elements, hence has cardinality 8. In general if a finite set (a set with a finite number of elements) has cardinality n , the power set of X has cardinality 2 n .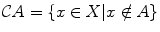
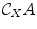 . The following properties are immediate:
. The following properties are immediate: 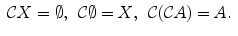
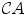 is the subset of odd numbers.
is the subset of odd numbers.