Cooke Roger - Mathematical Analysis II

Mathematical Analysis II — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Mathematical Analysis II" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...493

Springer-Verlag Berlin Heidelberg 2016

Vladimir A. Zorich Mathematical Analysis II Universitext 10.1007/978-3-662-48993-2_1

9. *Continuous Mappings (General Theory)

Vladimir A. Zorich 1

(1)

Department of Mathematics, Moscow State University, Moscow, Russia

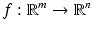In this chapter we shall generalize the properties of continuous mappings established earlier for numerical-valued functions and mappings of the type and discuss them from a unified point of view. In the process we shall introduce a number of simple, yet important concepts that are used everywhere in mathematics.

9.1 Metric Spaces

9.1.1 Definition and Examples

Definition 1

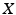A set is said to be endowed with a metric or a metric space structure or to be a metric space if a function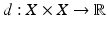

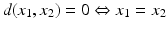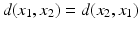(9.1)

is exhibited satisfying the following conditions:

a)

,

b)

(symmetry),

c)

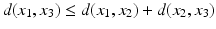(the triangle inequality),

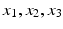where are arbitrary elements of .

In that case, the function () is called a metric or distance on .

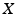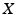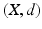Thus a metric space is a pair consisting of a set 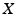and a metric defined on it.

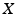In accordance with geometric terminology the elements of are called points .

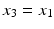We remark that if we set in the triangle inequality and take account of conditions a) and b) in the definition of a metric, we find that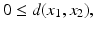

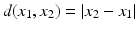that is, a distance satisfying axioms a), b), and c) is nonnegative.

Let us now consider some examples.

Example 1

The set of real numbers becomes a metric space if we set for any two numbers 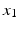and 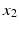, as we have always done.

Example 2

Other metrics can also be introduced on . A trivial metric, for example, is the discrete metric in which the distance between any two distinct points is 1.

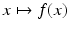The following metric on is much more substantive. Let be a nonnegative function defined for 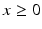and vanishing for 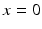. If this function is strictly convex upward, then, setting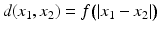

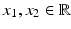(9.2)

for points , we obtain a metric on .

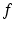Axioms a) and b) obviously hold here, and the triangle inequality follows from the easily verified fact that is strictly monotonic and satisfies the following inequalities for :

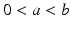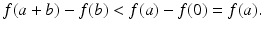
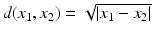In particular, one could set or 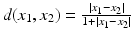. In the latter case the distance between any two points of the line is less than 1.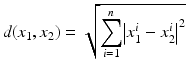

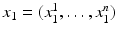Example 3

Besides the traditional distance

(9.3)

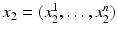between points and in 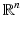, one can also introduce the distance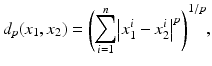

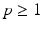(9.4)

where . The validity of the triangle inequality for the function () follows from Minkowskis inequality (see Sect. 5.4.2).

Example 4

When we encounter a word with incorrect letters while reading a text, we can reconstruct the word without too much trouble by correcting the errors, provided the number of errors is not too large. However, correcting the error and obtaining the word is an operation that is sometimes ambiguous. For that reason, other conditions being equal, one must give preference to the interpretation of the incorrect text that requires the fewest corrections. 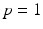Accordingly, in coding theory the metric () with is used on the set of all finite sequences of length 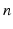consisting of zeros and ones.

Geometrically the set of such sequences can be interpreted as the set of vertices of the unit cube

Next page

1234567...493

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Mathematical Analysis II»

Look at similar books to Mathematical Analysis II. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

R. Cooke

Rome: Tempest of the Legion

Nick Clarke

Alistair Cooke

Jeff M. Phillips

Mathematical Foundations for Data Analysis

Julia Cooke

Come Fly the World

Cooke

History of Film Music

Claudio Canuto

Mathematical Analysis II

Claudio Canuto

Mathematical Analysis I

Shuxing Chen

Mathematical Analysis of Shock Wave Reflection

Alistair Cooke

Alistair Cooke at the Movies

Gazzola

Elements of Advanced Mathematical Analysis for Physics and Engineering

César Pérez López

MATLAB Mathematical Analysis

Roger Sworder

Mathematical Plato

Discussion, reviews of the book Mathematical Analysis II and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.