This is the first of three chapters dedicated to series. A series formalises the idea of adding infinitely many terms of a sequence which can involve numbers (numerical series) or functions (series of functions). Using series we can represent an irrational number by the sum of an infinite sequence of increasingly smaller rational numbers, for instance, or a continuous map by a sum of infinitely many piecewise-constant functions defined over intervals of decreasing size. Since the definition itself of series relies on the notion of limit of a sequence, the study of a series' behaviour requires all the instruments used for such limits.
In this chapter we will consider numerical series: beside their unquestionable theoretical importance, they serve as a warm-up for the ensuing study of series of functions. We begin by recalling their main properties. Subsequently we will consider the various types of convergence conditions of a numerical sequence and identify important classes of series, to study which the appropriate tools will be provided.
1.1 1.1 Round-up on sequences
We briefly recall here the definition and main properties of sequences, whose full treatise is present in Vol. I.
A real sequence is a function from to whose domain contains a set { n : n n 0} for some integer n 0 0. If one calls a the sequence, it is common practice to denote the image of n by a n instead of a ( n ); in other words we will write a : n a n . A standardised way to indicate a sequence is
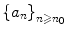
(ignoring the terms with n < n 0), or even more concisely { a n }.
The behaviour of a sequence as n tends to can be classified as follows. The sequence
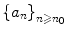
converges ( to l ) if the limit
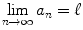
exists and is finite.
When the limit exists but is infinite, the sequence is said to diverge to + or . If the sequence is neither convergent nor divergent, i.e., if
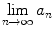
does not exist, the sequence is indeterminate .
The fact that the behaviour of the first terms is completely irrelevant justifies the following definition. A sequence
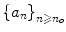
satisfies a certain property eventually , if there is an integer N n 0 such that the sequence { a n} n N satisfies the property.
The main theorems governing the limit behaviour of sequences are recalled below.
Let us review some cases of particular relevance.
Examples 1.1
i)
Consider the geometric sequence a n = q n , where q is a fixed number in . In Vol. I, Example 5.18, we proved
ii)
Let p > 0 be a given number and consider the sequence
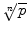
. Using the Substitution Theorem with g ( x ) = p x we have
iii)
Consider now
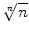
; again using the Substitution Theorem,
iv)
The number e may be defined as the limit of the sequence
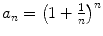
, which converges since it is strictly increasing and bounded from above.
v)
At last, look at the sequences, all tending to +,
In Vol. I, Sect. 5.4, we proved that each of these is infinite of order bigger than the preceding one. This means that for n , with > 0 and q < 1, we have
1.2 1.2 Numerical series
To introduce the notion of numerical series, i.e., of sum of infinitely many numbers , we examine a simple yet instructive situation borrowed from geometry.
Consider a segment of length = 2 (). The middle point splits it into two parts of length a 0 = /2 = 1. While keeping the left half fixed, we subdivide the right one in two parts of length a 1 = /4 = 1/2. Iterating the process indefinitely one can think of the initial segment as the union of infinitely many segments of lengths
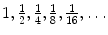
Correspondingly, the total length of the starting segment can be thought of as sum of the lengths of all sub-segments, in other words
Figure 1.1.
Successive splittings of the interval [0,2]. The coordinates of the subdivision points are indicated below the blue line, while the lengths of sub-intervals lie above it
Definition 1.2 Given the sequence { a k } k 0 and
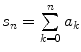
, consider the limit
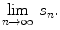
i)
If the limit exists ( finite or infinite ), its value s is called sum of the series and one writes
If s is finite, one says that the series
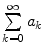
converges .














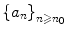 (ignoring the terms with n < n 0), or even more concisely { a n }.
(ignoring the terms with n < n 0), or even more concisely { a n }.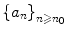 converges ( to l ) if the limit
converges ( to l ) if the limit 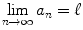 exists and is finite.
exists and is finite.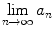 does not exist, the sequence is indeterminate .
does not exist, the sequence is indeterminate .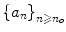 satisfies a certain property eventually , if there is an integer N n 0 such that the sequence { a n} n N satisfies the property.
satisfies a certain property eventually , if there is an integer N n 0 such that the sequence { a n} n N satisfies the property.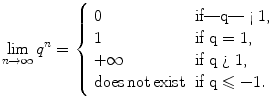
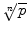 . Using the Substitution Theorem with g ( x ) = p x we have
. Using the Substitution Theorem with g ( x ) = p x we have 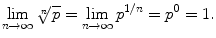
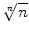 ; again using the Substitution Theorem,
; again using the Substitution Theorem, 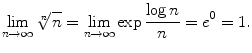
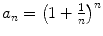 , which converges since it is strictly increasing and bounded from above.
, which converges since it is strictly increasing and bounded from above.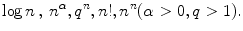
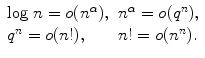
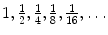 Correspondingly, the total length of the starting segment can be thought of as sum of the lengths of all sub-segments, in other words
Correspondingly, the total length of the starting segment can be thought of as sum of the lengths of all sub-segments, in other words 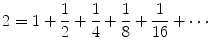

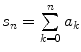 , consider the limit
, consider the limit 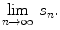
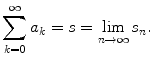
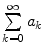 converges .
converges .