- 4 This is an old chestnut reheated.
- 6 Every number can be resolved into factors. If the only factors a number has are itself and 1, the number is said to be prime, e.g. 7 is a prime number, but 24 is not prime because: 24 = 6 x 4.
Any composite (non-prime) number can be resolved into factors which can be resolved in their turn until we end up with prime factors. Thus: 24 = 2 x 2 x 2 x 3 where all the numbers on the right are prime.
The set of prime numbers into which a number is resolved is unique. That is, 24 is the only number with 2, 2, 2 and 3 as its prime factors, and equally this is the only set of prime factors that 24 can be split into.
If a number is equal to the product of two prime numbers, it has no other factors. In this case, 118 = 2 x 59 and, as these are both prime numbers, they must be the only factors.
- 7 Consider the series: 1 + + +
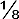 etc. At each stage the difference between the sum and the number 2 decreases. That is, the more fractions we add to the sequence, the closer the sum approaches 2. Strictly speaking, it will never get there as there is always a difference left to halve. But this difference can be made as small as we wish, so that in the end it is negligible.
etc. At each stage the difference between the sum and the number 2 decreases. That is, the more fractions we add to the sequence, the closer the sum approaches 2. Strictly speaking, it will never get there as there is always a difference left to halve. But this difference can be made as small as we wish, so that in the end it is negligible. The perceptive reader will ask at this point how it is that jumblium can lay claim to being the bounciest of all substances since it only bounced up to half the height of the previous bounce. The paradox is easily removed by pointing out that it exists in three forms. These are, in order of increasing bounciness, red, yellow and green. Puttylumps specimen was of red jumblium. The metals are used to colour the traffic lights on Zircon and since they are, in colour, closer to being orange, lemon and lime respectively, the natives of that planet speak of getting the lime-light instead of getting the green light. (See Hansoldts Whoopsy-Daisicon of Interplanetary Slang. )
- 9 Pembish was not too slow to realise that, although he could fill the bath in this way, it was not a practical way of going about things. Since the hot tap is slower, the bath water would get colder and colder as the bath filled. To get the temperature of the bath constant one would need to have the hot and cold taps running at the same rate.
Also, since the combined rate of water flowing into the bath was greater than the rate at which it left via the plughole, the bath would overflow. In the end he adopted the following strategy: he turned both taps on full. After six minutes the bath was half-full. He then turned the cold tap until it was running at the same rate as the hot tap. Then water was entering the bath at the same rate as it was leaving via the plughole and so it stayed exactly half-full. Since the hot and cold taps were flowing at the same rate, the temperature settled down to a temperature intermediate between the hot and the cold water, i.e. tepid. Luckily for him, the plug was discovered in the bread bin at this point and he was able to have a hot bath after all.
- 11 The ice-cube would fall without the buoyancy of the water, which must just balance the weight of the cube. Now, the amount of buoyancy must depend on the configuration of the water: i.e. the arrangement of the water in the glass. (If you were to press the cube lower into the water the buoyancy would increase.)
We can see how much buoyancy the water supplies in Fig. 12. It would just support the weight of water displaced by the ice-cube up to the surface in the diagram, or, in other words, the ice-cube and the water which would fill up to the dotted line if the cube were removed have the same weight. This means if the ice-cube were to melt it would produce as much water as would fill up to the dotted line, and thus would not alter the level of the water. Note that this argument applies only to the melting of ice which is afloat. If icebergs melt they do not affect the level of the sea. But if the polar ice-caps were to melt the water level would rise.
- 12 The boiling point of water is 212F (100C) and its freezing point is 32F (0C), so a change of 180 on the Fahrenheit scale is equivalent to a change of 100 on the Centigrade scale, that is, a change of 1F is equivalent to a change of
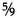 C.
C. The temperature in question must be below freezing point, for above freezing point the number of degrees Fahrenheit for a given temperature is always larger than the number of degrees Centigrade.
Suppose the answer is T C, then it must also be T F. Imagine cooling the jumblium from 32F down to 0F and then down to T F. This represents a cooling through
(32 + T ) Fahrenheit degrees. Each of these Fahrenheit degrees corresponds 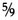 to Centigrade degrees.
to Centigrade degrees.
So the temperature is: 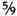 x (32 + T )C below zero, or:
x (32 + T )C below zero, or:
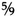 (32 + T ) = T . Multiplying both sides by 9 gives:
(32 + T ) = T . Multiplying both sides by 9 gives:
5 (32 + T ) = 9 T , or: 160 + 5 T = 9 T , whence T = 40. Therefore the temperature in question is 40C below zero, i.e. 40C or 40F.
- 15 More cumbersomely: if N be the number of eggs each hen lays in a day and H the number of hens the farmer has, then Puttylump has to solve the equation:
H N = N H
He knows that N and H must be integers as neither chickens nor eggs (no matter which came first) come in fractions. He discards the possibility that N = 1, otherwise there would be only one rather unremarkable hen, and anyway the farmer speaks of his charges as these ens.
He also discards the possibility that N = H. Then the equation would read:
H H = H H
which is true for all values of H , but there would be no change in the economy of feeding the hens if the number of hens and the number of eggs they each laid per day were interchanged.
Taking the next possible value for N, try N = 2. The equation becomes:
H 2 = 2 H
As the number on the right of this equation is even (since it is a power of 2), the number on the left-hand side must be even too. It follows that H must be even. Since H cannot be 2, we try the next even number, which is 4:
42 = 24
which is indeed true.
Thus, he has either two hens laying four eggs each per day, or four hens laying two eggs each per day. Either way they together lay eight eggs a day, but clearly, as it would be cheaper from the point of view of feeding them if there were two hens laying four eggs, the farmer must in fact have four hens laying two eggs each per day.
It is possible to prove mathematically that this is the only solution, but the proof is too long-winded for our present purposes.












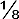 etc. At each stage the difference between the sum and the number 2 decreases. That is, the more fractions we add to the sequence, the closer the sum approaches 2. Strictly speaking, it will never get there as there is always a difference left to halve. But this difference can be made as small as we wish, so that in the end it is negligible.
etc. At each stage the difference between the sum and the number 2 decreases. That is, the more fractions we add to the sequence, the closer the sum approaches 2. Strictly speaking, it will never get there as there is always a difference left to halve. But this difference can be made as small as we wish, so that in the end it is negligible. 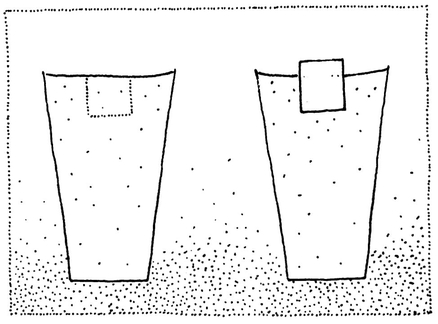
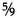 C.
C. 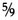 to Centigrade degrees.
to Centigrade degrees.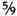 x (32 + T )C below zero, or:
x (32 + T )C below zero, or: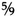 (32 + T ) = T . Multiplying both sides by 9 gives:
(32 + T ) = T . Multiplying both sides by 9 gives: