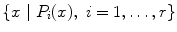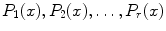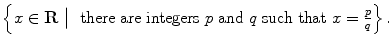Most of modern mathematics is expressed using the language of sets and functions. This can be a significant hurdle for the student whose mathematical experience, possibly through the entire calculus sequence, has not included any emphasis on sets or set operations. For that reason, we review these basic ideas in this chapter with the goal of both establishing the notation and providing a quick reference that the student can consult when proceeding through the main part of the text.
1.1 Sets
The basic concept that the notion of a set is meant to capture is that of inclusion or exclusion. Unfortunately, there are inherent logical difficulties in writing a formal definition of a set. We can resort to one standard definition: A set is a collection of objects. This gives a sense of both the distinction between the objects under consideration and the collection itself, as well as the sense of being included in the collection or not included. Unfortunately, it leaves undefined what is meant exactly by the terms collection and object, and so leaves much to be desired from the perspective of a mathematical definition.
For that reason, we will not try to be too precise in defining a set. Rather, we will call the objects under consideration elements , and we think of a set as something that contains elements.
We will generally use uppercase letters to denote sets: A , B , S , etc. We will write elements using lowercase letters: a , b , x , y , etc. We express the relation that x is an element of A by writing
We will sometimes more casually say, x is in A . If, on the contrary, an element y is not an element of the set A , we write
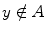
.
The basic assumption that we make about sets is that they are well defined : For every element x and every set A , the statement, Either x A or
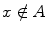
is true, and so the statement x A and
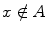
is false.
In any particular problem, the context will imply a universal set , which is the set of all objects under consideration. For example, statisticians might be concerned with a data set of measurements of heights in a given population of people. Geometers might be concerned with properties of the set of points in three-dimensional space. When the statisticians ask whether an element is in a particular set, they will consider only elements in their universe, and so in particular will not even ask the question whether the geometers points are in the statisticians sets.
While the universal set for a given discussion or problem may or may not be explicitly stated, it should always be able to be established from the context. From a logical point of view, in fact, the universal set is the context.
There are several standard ways of describing sets. The most basic way is by listing the elements, written using curly braces to enclose the elements of the set. For example, a set A with three elements a , b , and c is written
Note that the order in which the elements are listed is not important, so that, for example,
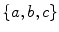
is the same set as
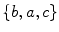
.
Describing a set by means of a list is also possible in the case of (countably) infinite sets, at least when there is a pattern involved. For example, the set of even natural numbers can be expressed as
Here, the ellipsis (
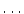
) expresses a pattern that should be obvious to the reader in context.
Most often, however, we will describe sets using what is known as set-builder notation . In this notation, a set is described as all elements (of the universal set) having a certain property or properties. These properties are generally given in the form of a logical statement about an element x , which we can write as P ( x ). In other words, P ( x ) is true if x has property P and P ( x ) is false if x does not have property P . Hence we write
to represent the set of all x in the universal set X for which the statement P ( x ) is true. When the universal set is clear from the context, we often simply write
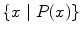
. In this notation, for example, the set of even natural numbers can be written
Here the statement P ( n ) is, there exists a natural number k such that n =2 k . Then P (4) is a true statement, since 4=2(2), and so 4 E . On the other hand, P (5) is false, since there is no natural number k such that 5=2 k , and so
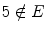
.
We will also encounter sets of elements described by several properties. For example, the set
means the set of all elements x for which the r distinct statements
are all true.
Set-builder notation has a number of advantages. First, it gives a way to effectively describe very large or infinite sets without having to resort to lists or cumbersome patterns. For example, the set of rational numbers can be described as















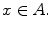
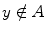 .
.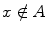 is true, and so the statement x A and
is true, and so the statement x A and 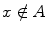 is false.
is false.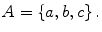
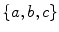 is the same set as
is the same set as 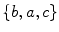 .
.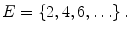
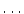 ) expresses a pattern that should be obvious to the reader in context.
) expresses a pattern that should be obvious to the reader in context.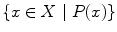
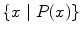 . In this notation, for example, the set of even natural numbers can be written
. In this notation, for example, the set of even natural numbers can be written 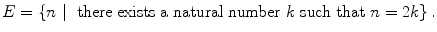
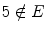 .
.