Peter Petersen - Riemannian Geometry
Here you can read online Peter Petersen - Riemannian Geometry full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: Cham, publisher: Springer International Publishing, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Riemannian Geometry
- Author:
- Publisher:Springer International Publishing
- Genre:
- City:Cham
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
- 60
- 1
- 2
- 3
- 4
- 5
Riemannian Geometry: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Riemannian Geometry" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Riemannian Geometry — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Riemannian Geometry" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
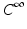 -manifold M (Hausdorff and second countable) and a Euclidean inner product g p or g | p on each of the tangent spaces T p M of M . In addition we assume that p g p varies smoothly. This means that for any two smooth vector fields X , Y the inner product
-manifold M (Hausdorff and second countable) and a Euclidean inner product g p or g | p on each of the tangent spaces T p M of M . In addition we assume that p g p varies smoothly. This means that for any two smooth vector fields X , Y the inner product 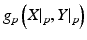 is a smooth function of p .The subscript p will usually be suppressed when it is not needed. Thus we might write
is a smooth function of p .The subscript p will usually be suppressed when it is not needed. Thus we might write 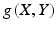 with the understanding that this is to be evaluated at each p where X and Y are defined. When we wish to associate the metric with M we also denote it as g M .The tensor g is referred to as the Riemannian metric or simply the metric . Generally speaking the manifold is assumed to be connected. Exceptions do occur, especially when studying level sets or submanifolds defined by constraints.
with the understanding that this is to be evaluated at each p where X and Y are defined. When we wish to associate the metric with M we also denote it as g M .The tensor g is referred to as the Riemannian metric or simply the metric . Generally speaking the manifold is assumed to be connected. Exceptions do occur, especially when studying level sets or submanifolds defined by constraints.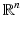 with its canonical inner product. Hence, all Riemannian manifolds have the same infinitesimal structure not only as manifolds but also as Riemannian manifolds.
with its canonical inner product. Hence, all Riemannian manifolds have the same infinitesimal structure not only as manifolds but also as Riemannian manifolds.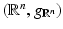 . The canonical Riemannian structure
. The canonical Riemannian structure 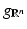 is defined by the tangent bundle identification
is defined by the tangent bundle identification 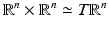 given by the map:
given by the map: 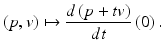
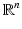 is defined by
is defined by 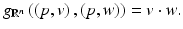
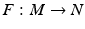 such that F g N = g M ,i.e.,
such that F g N = g M ,i.e., 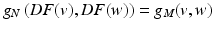
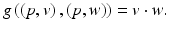
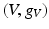 and
and 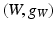 of the same dimension, then they are isometric. A example of a Riemannian isometry
of the same dimension, then they are isometric. A example of a Riemannian isometry 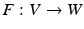
Font size:
Interval:
Bookmark:
Similar books «Riemannian Geometry»
Look at similar books to Riemannian Geometry. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book Riemannian Geometry and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.













