Real Variables with Basic Metric Space Topology
INTRODUCTION
1.1BASIC TERMINOLOGY
In a course in real analysis, the normal procedure is to begin with a definition of the real numbers, either by means of a set of axioms or by a constructive procedure which starts with the Godgiven set of positive integers. The set of all integers is constructed, and from this the rational numbers are obtained, and finally the reals. A discussion of this type is part of the area of logic and foundations rather than real analysis, and we will postpone it until much later. For now well take the point of view that we know what the real numbers are: A real number is an integer plus an infinite decimal, for example, 65.7204
If the decimal ends in all nines, we have two representations of the same real number, for example,
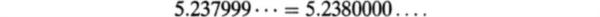
We will often talk about sets of real numbers, and therefore a modest amount of settheoretic terminology is necessary before we can get anywhere. You have probably seen most of this in another course, so we will proceed rather quickly.
1.1.1Definitions and Comments
The union of two sets A and B, denoted by AB, is the set of points belonging to either A or B (or both; from now on, the word or always has the socalled inclusive connotation or both unless otherwise specified).
The intersection of two sets A and B, denoted by AB, is the set of points belonging to both A and B.
The complement of a set A, denoted by Ac, is the set of points not belonging to A. (Generally, we will be working in a fixed space (sometimes called the universe), for example, the set of real numbers or perhaps the set of pairs of real numbers, that is, the Euclidean plane. All sets under discussion will consist of various points of , and thus Ac is the set of points of that do not belong to A).
Unions, intersections, and complements may be represented by pictures called Venn diagrams that are probably familiar to many readers; see .
Unions and intersections may be defined for more than two sets, in fact for an arbitrary collection of sets.
The union of sets A1, A2,, denoted by A1A2 or by 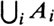 , is the set of points belonging to at least one of the A1; the intersection of A1, A2,, denoted by A12 or by
, is the set of points belonging to at least one of the A1; the intersection of A1, A2,, denoted by A12 or by 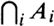 , is the set of points belonging to all the Ai. The union of sets A1, , An is often written as
, is the set of points belonging to all the Ai. The union of sets A1, , An is often written as 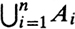 , and the union of an infinite sequence A1, A2, is denoted by
, and the union of an infinite sequence A1, A2, is denoted by 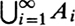 , with similar notation for intersection.
, with similar notation for intersection.
There are a few identities involving unions, intersections, and complements that come up occasionally. For example, the distributive law holds: for arbitrary sets A, B, C,
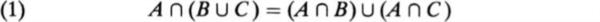
(the word distributive is used because in this formula, at least, intersection behaves like ordinary multiplication and union like addition).
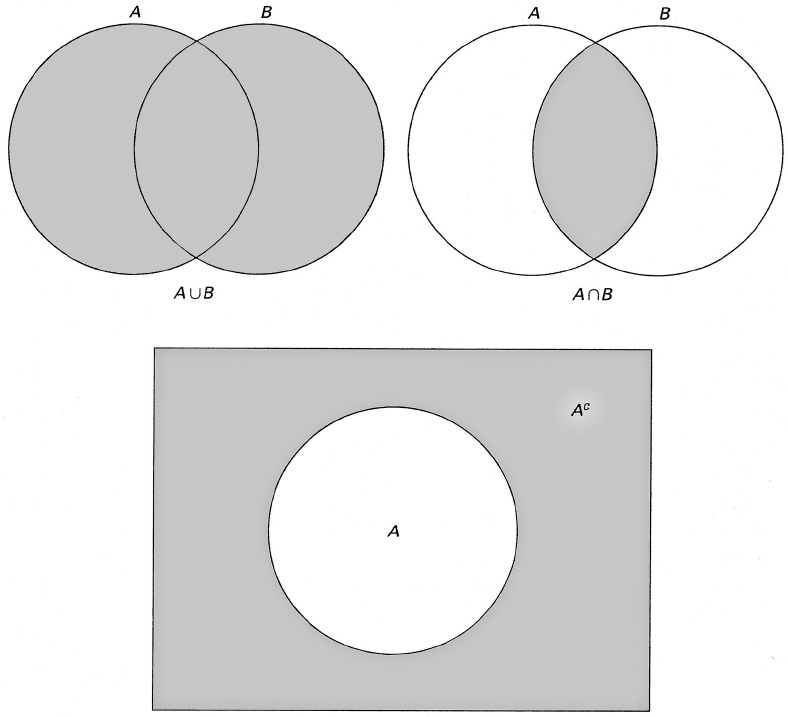
Figure 1.1.1 Union, Intersection, and Complement
) or by showing that the sets on the left and right sides of the equality have the same members, as follows. (The symbol means belongs to.) If xA (BC), then xA and xBC, so that xB or xC.
Case 1.xA and xB; then xAB; hence x (AB) (A C).
Case 2.xA and xC ; then xAC; hence x (AB) (AC).
Caution. So far we have shown only that the set on the left is a subset of the set on the right. In general, the set D is said to be a subset of the set E if every point of D also belongs to E (see ). We use the notation DE ; sometimes we say that E contains D or the D is contained in E. In order to show that D = E we must also show that every point of E belongs to D. If DE but DE, we say that D is a proper subset of E, sometimes written DE. Note that according to the definition, a set is a subset of itself.
To return to the proof of the distributive law, suppose x (AB) (AC). Then xAB or xAC; thus, we know definitely that xA, and also xB or xC, as desired.
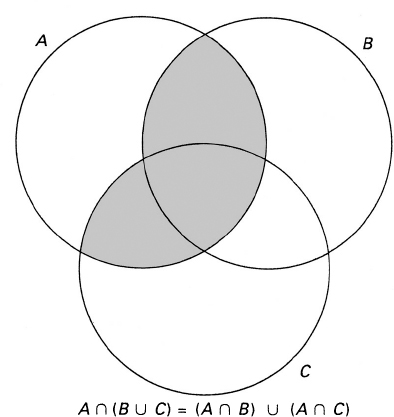
Figure 1.1.2 Distributive Law
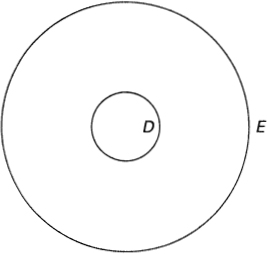
Figure 1.1.3 Subset Relation
The following identities, called the De Morgan laws, are often useful:
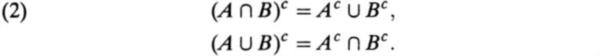
As above, the identities can be verified by a Venn diagram or a formal argument using the definitions of union, intersection, and complement. In fact the De Morgan laws can be extended to an arbitrary collection of sets, as follows:
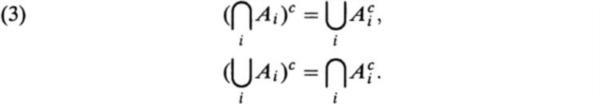
The Venn diagram approach is not useful with such a large collection of sets, and the formal method must be used ().
To complete the necessary set-theoretic terminology, the empty set (set with no members) will be denoted by 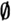 . If A is any set, then
. If A is any set, then 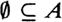 . (If you produce an element
. (If you produce an element 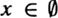 , I will be delighted to show that x belongs to A.) We will look at this idea in more detail in . The sets Ai are said to be disjoint or mutually exclusive if there is no overlap between any pair of sets; that is,
, I will be delighted to show that x belongs to A.) We will look at this idea in more detail in . The sets Ai are said to be disjoint or mutually exclusive if there is no overlap between any pair of sets; that is,
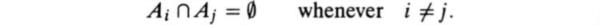
As an example, let A = {1, 2, 3}, B = {1, 2}, C = {3, 5} (the notation is standard: a set is described by listing its members, so that, for example, A is the set consisting of the numbers 1, 2, and 3). In this case,
Next page














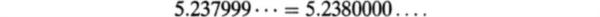
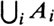 , is the set of points belonging to at least one of the A1; the intersection of A1, A2,, denoted by A12 or by
, is the set of points belonging to at least one of the A1; the intersection of A1, A2,, denoted by A12 or by 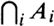 , is the set of points belonging to all the Ai. The union of sets A1, , An is often written as
, is the set of points belonging to all the Ai. The union of sets A1, , An is often written as 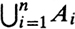 , and the union of an infinite sequence A1, A2, is denoted by
, and the union of an infinite sequence A1, A2, is denoted by 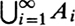 , with similar notation for intersection.
, with similar notation for intersection.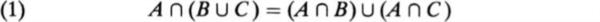



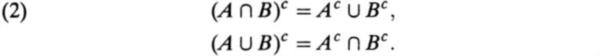
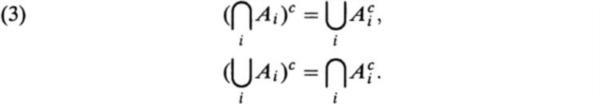
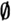 . If A is any set, then
. If A is any set, then 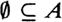 . (If you produce an element
. (If you produce an element 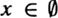 , I will be delighted to show that x belongs to A.) We will look at this idea in more detail in . The sets Ai are said to be disjoint or mutually exclusive if there is no overlap between any pair of sets; that is,
, I will be delighted to show that x belongs to A.) We will look at this idea in more detail in . The sets Ai are said to be disjoint or mutually exclusive if there is no overlap between any pair of sets; that is,