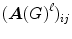Richard P. Stanley Undergraduate Texts in Mathematics Algebraic Combinatorics 2013 Walks, Trees, Tableaux, and More 10.1007/978-1-4614-6998-8_1 Springer Science+Business Media New York 2013
1. Walks in Graphs
Abstract
Given a finite set S and integer k 0, let
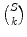
denote the set of k -element subsets of S . A multiset may be regarded, somewhat informally, as a set with repeated elements, such as {1,1,3,4,4,4,6,}. We are only concerned with how many times each element occurs and not on any ordering of the elements. Thus for instance {2,1,2,4,1,2} and {1,1,2,2,2,4} are the same multiset: they each contain two 1s, three 2s, and one 4 (and no other elements).
Given a finite set S and integer k 0, let
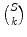
denote the set of k -element subsets of S . A multiset may be regarded, somewhat informally, as a set with repeated elements, such as {1,1,3,4,4,4,6,6}. We are only concerned with how many times each element occurs and not on any ordering of the elements. Thus for instance {2,1,2,4,1,2} and {1,1,2,2,2,4} are the same multiset: they each contain two 1s, three 2s, and one 4 (and no other elements). We say that a multiset M is on a set S if every element of M belongs to S . Thus the multiset in the example above is on the set S ={ 1,3,4,6} and also on any set containing S . Let
denote the set of k -element multisets on S . For instance, if S ={ 1,2,3} then (using abbreviated notation),
We now define what is meant by a graph. Intuitively, graphs have vertices and edges, where each edge connects two vertices (which may be the same). It is possible for two different edges e and e to connect the same two vertices. We want to be able to distinguish between these two edges, necessitating the following more precise definition. A (finite) graphG consists of a vertex set
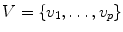
and edge set
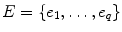
, together with a function
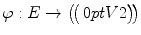
. We think that if ( e )= uv (short for { u , v }), then e connects u and v or equivalently e is incident to u and v . If there is at least one edge incident to u and v then we say that the vertices u and v are adjacent . If ( e )= vv , then we call e a loop at v . If several edges

( j >1) satisfy
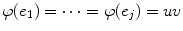
, then we say that there is a multiple edge between u and v . A graph without loops or multiple edges is called simple . In this case we can think of E as just a subset of
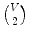
[why?].
The adjacency matrix of the graph G is the p p matrix
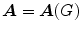
, over the field of complex numbers, whose ( i , j )-entry a ij is equal to the number of edges incident to v i and v j . Thus
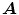
is a real symmetric matrix (and hence has real eigenvalues) whose trace is the number of loops in G . For instance, if G is the graph
A walk in G of length from vertex u to vertex v is a sequence
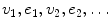
, v , e , v +1 such that:
Each v i is a vertex of G .
Each e j is an edge of G .
The vertices of e i are v i and v i +1, for 1 i .
v 1= u and
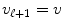
.
1.1 Theorem.
For any integer 1, the (i,j)-entry of the matrix
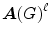
is equal to the number of walks from v i to v j in G of length .
Proof.
This is an immediate consequence of the definition of matrix multiplication. Let
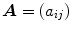
. The ( i , j )-entry of
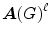
is given by
where the sum ranges over all sequences
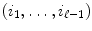
with 1 i k p . But since a rs is the number of edges between v r and v s , it follows that the summand
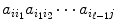
in the above sum is just the number (which may be 0) of walks of length from v i to v j of the form
(since there are
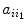
choices for e 1,
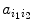
choices for e 2, etc.) Hence summing over all
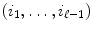
just gives the total number of walks of length from v i to v j , as desired.
We wish to use Theorem 1.1 to obtain an explicit formula for the number
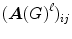

















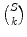 denote the set of k -element subsets of S . A multiset may be regarded, somewhat informally, as a set with repeated elements, such as {1,1,3,4,4,4,6,}. We are only concerned with how many times each element occurs and not on any ordering of the elements. Thus for instance {2,1,2,4,1,2} and {1,1,2,2,2,4} are the same multiset: they each contain two 1s, three 2s, and one 4 (and no other elements).
denote the set of k -element subsets of S . A multiset may be regarded, somewhat informally, as a set with repeated elements, such as {1,1,3,4,4,4,6,}. We are only concerned with how many times each element occurs and not on any ordering of the elements. Thus for instance {2,1,2,4,1,2} and {1,1,2,2,2,4} are the same multiset: they each contain two 1s, three 2s, and one 4 (and no other elements).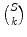 denote the set of k -element subsets of S . A multiset may be regarded, somewhat informally, as a set with repeated elements, such as {1,1,3,4,4,4,6,6}. We are only concerned with how many times each element occurs and not on any ordering of the elements. Thus for instance {2,1,2,4,1,2} and {1,1,2,2,2,4} are the same multiset: they each contain two 1s, three 2s, and one 4 (and no other elements). We say that a multiset M is on a set S if every element of M belongs to S . Thus the multiset in the example above is on the set S ={ 1,3,4,6} and also on any set containing S . Let
denote the set of k -element subsets of S . A multiset may be regarded, somewhat informally, as a set with repeated elements, such as {1,1,3,4,4,4,6,6}. We are only concerned with how many times each element occurs and not on any ordering of the elements. Thus for instance {2,1,2,4,1,2} and {1,1,2,2,2,4} are the same multiset: they each contain two 1s, three 2s, and one 4 (and no other elements). We say that a multiset M is on a set S if every element of M belongs to S . Thus the multiset in the example above is on the set S ={ 1,3,4,6} and also on any set containing S . Let 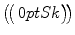 denote the set of k -element multisets on S . For instance, if S ={ 1,2,3} then (using abbreviated notation),
denote the set of k -element multisets on S . For instance, if S ={ 1,2,3} then (using abbreviated notation), 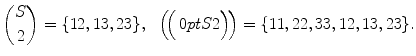
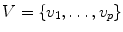 and edge set
and edge set 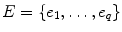 , together with a function
, together with a function 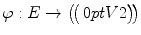 . We think that if ( e )= uv (short for { u , v }), then e connects u and v or equivalently e is incident to u and v . If there is at least one edge incident to u and v then we say that the vertices u and v are adjacent . If ( e )= vv , then we call e a loop at v . If several edges
. We think that if ( e )= uv (short for { u , v }), then e connects u and v or equivalently e is incident to u and v . If there is at least one edge incident to u and v then we say that the vertices u and v are adjacent . If ( e )= vv , then we call e a loop at v . If several edges  ( j >1) satisfy
( j >1) satisfy 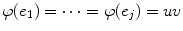 , then we say that there is a multiple edge between u and v . A graph without loops or multiple edges is called simple . In this case we can think of E as just a subset of
, then we say that there is a multiple edge between u and v . A graph without loops or multiple edges is called simple . In this case we can think of E as just a subset of 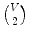 [why?].
[why?].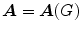 , over the field of complex numbers, whose ( i , j )-entry a ij is equal to the number of edges incident to v i and v j . Thus
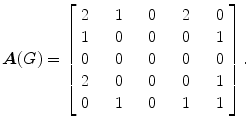
, over the field of complex numbers, whose ( i , j )-entry a ij is equal to the number of edges incident to v i and v j . Thus 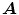 is a real symmetric matrix (and hence has real eigenvalues) whose trace is the number of loops in G . For instance, if G is the graph
is a real symmetric matrix (and hence has real eigenvalues) whose trace is the number of loops in G . For instance, if G is the graph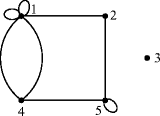
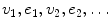 , v , e , v +1 such that:
, v , e , v +1 such that: 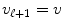 .
.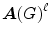 is equal to the number of walks from v i to v j in G of length .
is equal to the number of walks from v i to v j in G of length .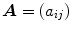 . The ( i , j )-entry of
. The ( i , j )-entry of 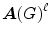 is given by
is given by 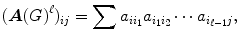
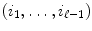 with 1 i k p . But since a rs is the number of edges between v r and v s , it follows that the summand
with 1 i k p . But since a rs is the number of edges between v r and v s , it follows that the summand 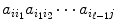 in the above sum is just the number (which may be 0) of walks of length from v i to v j of the form
in the above sum is just the number (which may be 0) of walks of length from v i to v j of the form 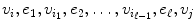
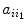 choices for e 1,
choices for e 1, 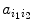 choices for e 2, etc.) Hence summing over all
choices for e 2, etc.) Hence summing over all 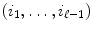 just gives the total number of walks of length from v i to v j , as desired.
just gives the total number of walks of length from v i to v j , as desired.