Boolean AlgebraBoolean Algebra R. L. Goodstein Dover Publications, Inc. Mineola, New York Bibliographical Note This Dover edition, first published in 2007, is an unabridged republication of the 1966 printing of the work originall published by Pergamon Press,London, in 1963 International Standard Book Number:ISBN-13: 978-0-4861-54978 Manufactured in the United States by Courier Corporation 45894602 www.doverpublications.com Preface A FTER an informal introduction to the algebra of classes, three different axiomatizations are studied in some detail, and an outline of a fourth system of axioms is given in the examples. In the last chapter Boolean algebra is examined in the setting of the theory of partial order. The treatment is entirely elementary and my aim has been to use Boolean algebra as a simple medium for introducing important concepts of modern algebra. There is a large collection of examples, with full solutions at the end of the book.
I have used the symbols  ,
,  for union and intersection, but I have not introduced their current readings cup and cap, which I find so unhelpful. I myself prefer to read A
for union and intersection, but I have not introduced their current readings cup and cap, which I find so unhelpful. I myself prefer to read A  B as A and B and A
B as A and B and A  B as A or B since the members of A
B as A or B since the members of A  B are the member of A or of B, and the members of A
B are the member of A or of B, and the members of A  B are members of A and of B, and of course this reading is in conformity with the interpretation of Boolean algebra as an algebra of sentences. I am happy to record my thanks to Mr. M. T. R. L. L.
B are members of A and of B, and of course this reading is in conformity with the interpretation of Boolean algebra as an algebra of sentences. I am happy to record my thanks to Mr. M. T. R. L. L.
G OODSTEIN. University of Leicester. CHAPTER ONE The informal algebra of classes 1.0. Classes. Collections of objects, whether they are identified by a survey of their members or by means of some characteristic property which their members have, are called classes. The students in a particular room at a particular time form a class, the voters on an electoral roll of a certain town form a class (as do their names on the roll), the hairs on a mans head, the blood-cells in his body, the seconds of time he has lived, all these form classes. 1.1. Membership. We shall use capital letters as names of classes. Membership. We shall use capital letters as names of classes.
If an object a is a member of a class A we shall write 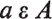 and say that a belongs to A, or a is in A. The membership symbol (the Greek letter ) is the initial letter of the Greek verb to be. Thus Earth Planets expresses the relationship of our earth to the class of planets. If a is not a member of a class A then we write
and say that a belongs to A, or a is in A. The membership symbol (the Greek letter ) is the initial letter of the Greek verb to be. Thus Earth Planets expresses the relationship of our earth to the class of planets. If a is not a member of a class A then we write 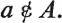 If we can write down signs for all the members of a class we represent this class by enclosing the signs in brackets. Thus {1, 2, 3} is the class containing the numbers 1, 2 and 3 (and nothing else), {2, 1, 3}, {3, 1, 2} {1, 1, 2, 3} for instance denoting the same class, and {a, b, c, d} is the class containing just the first four letters of the alphabet. We can represent any fairly small class in this way, but the notation is obviously impractical for large classes (like the class of all numbers from 1 to 1010) and meaningless for classes with an unlimited supply of members (like the class of all whole numbers).
If we can write down signs for all the members of a class we represent this class by enclosing the signs in brackets. Thus {1, 2, 3} is the class containing the numbers 1, 2 and 3 (and nothing else), {2, 1, 3}, {3, 1, 2} {1, 1, 2, 3} for instance denoting the same class, and {a, b, c, d} is the class containing just the first four letters of the alphabet. We can represent any fairly small class in this way, but the notation is obviously impractical for large classes (like the class of all numbers from 1 to 1010) and meaningless for classes with an unlimited supply of members (like the class of all whole numbers).
The class whose sole member is some object A, namely the class {A}, must be distinguished from A itself. For instance if A = {1,2} then {A} is a class with only one member, but A is a class with two members. A class with a single member is called a unit class. The Master of Trinity is a unit class, and so is The Queen of England. 1.2. Inclusion. If every member of a class A is also a member of a class B we say that the class A is contained in the class B, or A is included in B, and write 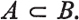 It is important to distinguish between the membership relation and the inclusion relation
It is important to distinguish between the membership relation and the inclusion relation  .
.
The membership relation is the relation in which a member of a class stands to the class itself; on one side (the left) of the membership relation stands a class member, and on the other side (the right) stands a class. But inclusion is a relation between classes, and a class stands on each side of the relation of inclusion. If A B, we say that A is a subclass of B, and that B is a superclass of A. Every class is included in itself, thus A
B, we say that A is a subclass of B, and that B is a superclass of A. Every class is included in itself, thus A A, because the members of A (on the left) are necessarily members of the same class A (on the right). A subclass of a class A which is not just A itself, is called a proper subclass. 1.3. The empty class and the universal class. A convenient fiction is the empty, or null class, the class without members. The empty class and the universal class. A convenient fiction is the empty, or null class, the class without members.
A, because the members of A (on the left) are necessarily members of the same class A (on the right). A subclass of a class A which is not just A itself, is called a proper subclass. 1.3. The empty class and the universal class. A convenient fiction is the empty, or null class, the class without members. The empty class and the universal class. A convenient fiction is the empty, or null class, the class without members.
If no candidate presents himself for some examination, the class of candidates is the empty class. We denote the empty class by 0; thus the relation x 0 is false for every object x in the world. Another convenient fiction is the universal class, the class of everything (or everything under consideration) which we denote by 1. The null class and the universal class are each unique. The null class is considered to be a subclass of every class (for there is no object which is a member of 0 and not a member of any A). Any class is of course a subclass of the universal class.
In particular 0  l. 1.4. The complement of a class. If we remove from the universal class all the members of some class A, the objects which remain form the class complement of A, denoted by A. The classes A, A have no members in common, but everything in the universal class is either a member of A or a member of A. The complement of the null class is the universal class, and conversely the complement of the universal class is the null class. 1.5 Union and intersection. Given two classes A, B we may form the class C, called the union of A and B whose members are precisely those objects which are members of A or members of B ; if A and B have any members in common, these common members occur once only in the union. 1.5 Union and intersection. Given two classes A, B we may form the class C, called the union of A and B whose members are precisely those objects which are members of A or members of B ; if A and B have any members in common, these common members occur once only in the union.
l. 1.4. The complement of a class. If we remove from the universal class all the members of some class A, the objects which remain form the class complement of A, denoted by A. The classes A, A have no members in common, but everything in the universal class is either a member of A or a member of A. The complement of the null class is the universal class, and conversely the complement of the universal class is the null class. 1.5 Union and intersection. Given two classes A, B we may form the class C, called the union of A and B whose members are precisely those objects which are members of A or members of B ; if A and B have any members in common, these common members occur once only in the union. 1.5 Union and intersection. Given two classes A, B we may form the class C, called the union of A and B whose members are precisely those objects which are members of A or members of B ; if A and B have any members in common, these common members occur once only in the union.
For instance if A and B are sacks of potatoes their union is formed by emptying both sacks into a third. The union of two classes
Next page









 ,
,  for union and intersection, but I have not introduced their current readings cup and cap, which I find so unhelpful. I myself prefer to read A
for union and intersection, but I have not introduced their current readings cup and cap, which I find so unhelpful. I myself prefer to read A 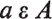 and say that a belongs to A, or a is in A. The membership symbol (the Greek letter ) is the initial letter of the Greek verb to be. Thus Earth Planets expresses the relationship of our earth to the class of planets. If a is not a member of a class A then we write
and say that a belongs to A, or a is in A. The membership symbol (the Greek letter ) is the initial letter of the Greek verb to be. Thus Earth Planets expresses the relationship of our earth to the class of planets. If a is not a member of a class A then we write 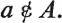 If we can write down signs for all the members of a class we represent this class by enclosing the signs in brackets. Thus {1, 2, 3} is the class containing the numbers 1, 2 and 3 (and nothing else), {2, 1, 3}, {3, 1, 2} {1, 1, 2, 3} for instance denoting the same class, and {a, b, c, d} is the class containing just the first four letters of the alphabet. We can represent any fairly small class in this way, but the notation is obviously impractical for large classes (like the class of all numbers from 1 to 1010) and meaningless for classes with an unlimited supply of members (like the class of all whole numbers).
If we can write down signs for all the members of a class we represent this class by enclosing the signs in brackets. Thus {1, 2, 3} is the class containing the numbers 1, 2 and 3 (and nothing else), {2, 1, 3}, {3, 1, 2} {1, 1, 2, 3} for instance denoting the same class, and {a, b, c, d} is the class containing just the first four letters of the alphabet. We can represent any fairly small class in this way, but the notation is obviously impractical for large classes (like the class of all numbers from 1 to 1010) and meaningless for classes with an unlimited supply of members (like the class of all whole numbers).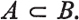 It is important to distinguish between the membership relation and the inclusion relation
It is important to distinguish between the membership relation and the inclusion relation  .
.