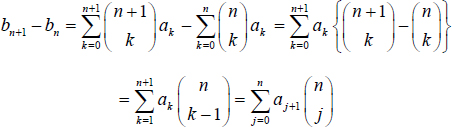Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office : 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE British Library Cataloguing-in-Publication Data A catalogue record for this book is available from the British Library. NOTES ON THE BINOMIAL TRANSFORM
Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office : 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE British Library Cataloguing-in-Publication Data A catalogue record for this book is available from the British Library. NOTES ON THE BINOMIAL TRANSFORM
Theory and Table with Appendix on Stirling Transform Copyright 2018 by World Scientific Publishing Co. Ltd. Ltd.
All rights reserved. This book, or parts thereof, may not be reproduced in any form or by any means, electronic or mechanical, including photocopying, recording or any information storage and retrieval system now known or to be invented, without written permission from the publisher. For photocopying of material in this volume, please pay a copying fee through the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, USA. In this case permission to photocopy is not required from the publisher. ISBN 978-981-3234-97-0 For any available supplementary material, please visit
http://www.worldscientifc.com/worldscibooks/10.1142/10848#t=suppl Printed in Singapore This book is dedicated to my wife Irina and daughters Marinella and Alexandra. Preface The binomial transform is a discrete transformation of one sequence into another with many interesting applications in combinatorics and analysis.
The binomial transform theory belongs to the expanding field of discrete mathematics. The material of this book will be helpful to researchers interested in enumerative combinatorics, special numbers, and classical analysis. The book can also serve as a valuable reference. It can be used as lecture notes for a course on binomial identities, binomial transforms and Euler series transformations. The binomial transform leads to various combinatorial and analytical identities involving binomial coefficients. Many interesting identities can be written as binomial transforms and vice versa.
The book consists of two parts. In the first part, we present the theory of the binomial transform for sequences with a sufficient prerequisite of classical numbers and polynomials. The first part provides theorems and tools which help to compute binomial transforms of different sequences and also to generate new binomial identities from old. These theoretical tools (formulas and theorems) can also be used for summation of series and various numerical computations. In the second part, we have compiled a list of binomial transform formulas for easy reference. Contents Part 1 Theory of the Binomial Transform Chapter 1 Introduction We assume basic knowledge about the binomial coefficients 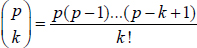 and throughout we use the agreement that
and throughout we use the agreement that 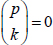 if k < 0. Contents Part 1 Theory of the Binomial Transform Chapter 1 Introduction We assume basic knowledge about the binomial coefficients
if k < 0. Contents Part 1 Theory of the Binomial Transform Chapter 1 Introduction We assume basic knowledge about the binomial coefficients 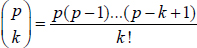 and throughout we use the agreement that
and throughout we use the agreement that 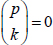 if k < 0.
if k < 0.
Here p does not need to be an integer. Now we define the binomial transform. Given a sequence {ak}, k = 0,1,2, its binomial transform is the new sequence {bn}, n = 0,1,2 generated by the formula  with inversion
with inversion 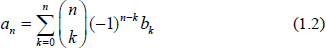 which can be written also as
which can be written also as 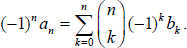 The symmetric version of the binomial transform is used very often. In this case the sequence {bk} is defined by
The symmetric version of the binomial transform is used very often. In this case the sequence {bk} is defined by 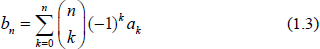 and the inversion formula is
and the inversion formula is 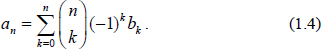 Here the factor (1)k can be replaced by (1)k1. A simple computation shows that (1.3) implies the formula
Here the factor (1)k can be replaced by (1)k1. A simple computation shows that (1.3) implies the formula 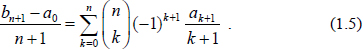 If the sequence {ak} is indexed from k = 1,2, we can assume that a0 = 0 in order to use the same formulas. In this case we have also b0 = 0.
If the sequence {ak} is indexed from k = 1,2, we can assume that a0 = 0 in order to use the same formulas. In this case we have also b0 = 0.
Here is a proof of the inversion formula (1.2). 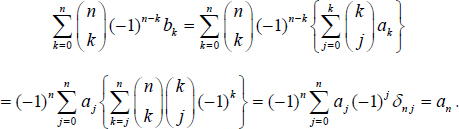 Here the last equality follows from the convolution identity
Here the last equality follows from the convolution identity 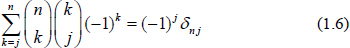 where nj is the Kronecker symbol. The inversion formula (1.4) follows from (1.2) as we can write
where nj is the Kronecker symbol. The inversion formula (1.4) follows from (1.2) as we can write 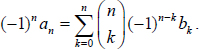 The binomial transform naturally appears in the theory of finite differences. Let
The binomial transform naturally appears in the theory of finite differences. Let 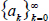 be a sequence and consider the forward difference operator defined by ak = ak+1ak. It is easy to compute that
be a sequence and consider the forward difference operator defined by ak = ak+1ak. It is easy to compute that 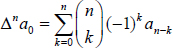 and because of the well-known property
and because of the well-known property 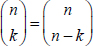 this can be written also as
this can be written also as 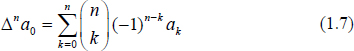 or, equivalently, as
or, equivalently, as 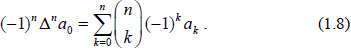 Another elementary property involves the transform of the shifted sequence. If (1.1) is true then
Another elementary property involves the transform of the shifted sequence. If (1.1) is true then 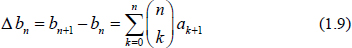 for n 1 (see []).
for n 1 (see []).
Here is the simple proof 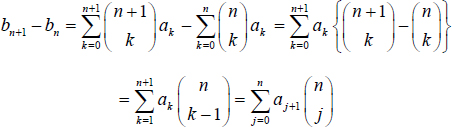
Next page











 Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office : 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE British Library Cataloguing-in-Publication Data A catalogue record for this book is available from the British Library. NOTES ON THE BINOMIAL TRANSFORM
Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224 USA office : 27 Warren Street, Suite 401-402, Hackensack, NJ 07601 UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE British Library Cataloguing-in-Publication Data A catalogue record for this book is available from the British Library. NOTES ON THE BINOMIAL TRANSFORM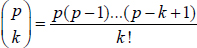 and throughout we use the agreement that
and throughout we use the agreement that 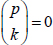 if k < 0. Contents Part 1 Theory of the Binomial Transform Chapter 1 Introduction We assume basic knowledge about the binomial coefficients
if k < 0. Contents Part 1 Theory of the Binomial Transform Chapter 1 Introduction We assume basic knowledge about the binomial coefficients  with inversion
with inversion 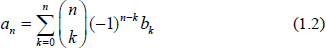 which can be written also as
which can be written also as 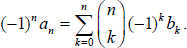 The symmetric version of the binomial transform is used very often. In this case the sequence {bk} is defined by
The symmetric version of the binomial transform is used very often. In this case the sequence {bk} is defined by 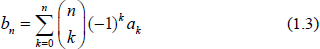 and the inversion formula is
and the inversion formula is 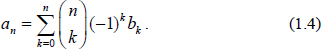 Here the factor (1)k can be replaced by (1)k1. A simple computation shows that (1.3) implies the formula
Here the factor (1)k can be replaced by (1)k1. A simple computation shows that (1.3) implies the formula 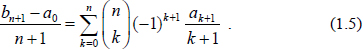 If the sequence {ak} is indexed from k = 1,2, we can assume that a0 = 0 in order to use the same formulas. In this case we have also b0 = 0.
If the sequence {ak} is indexed from k = 1,2, we can assume that a0 = 0 in order to use the same formulas. In this case we have also b0 = 0.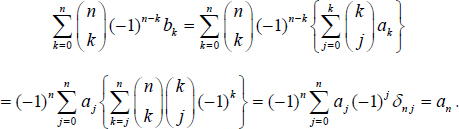 Here the last equality follows from the convolution identity
Here the last equality follows from the convolution identity 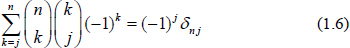 where nj is the Kronecker symbol. The inversion formula (1.4) follows from (1.2) as we can write
where nj is the Kronecker symbol. The inversion formula (1.4) follows from (1.2) as we can write 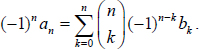 The binomial transform naturally appears in the theory of finite differences. Let
The binomial transform naturally appears in the theory of finite differences. Let 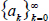 be a sequence and consider the forward difference operator defined by ak = ak+1ak. It is easy to compute that
be a sequence and consider the forward difference operator defined by ak = ak+1ak. It is easy to compute that 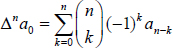 and because of the well-known property
and because of the well-known property 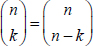 this can be written also as
this can be written also as 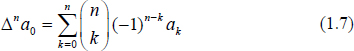 or, equivalently, as
or, equivalently, as 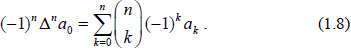 Another elementary property involves the transform of the shifted sequence. If (1.1) is true then
Another elementary property involves the transform of the shifted sequence. If (1.1) is true then 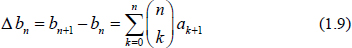 for n 1 (see []).
for n 1 (see []).