Lancelot Hogben - Mathematics for the Million
Here you can read online Lancelot Hogben - Mathematics for the Million full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. publisher: W. W. Norton & Company, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Mathematics for the Million
- Author:
- Publisher:W. W. Norton & Company
- Genre:
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
- 60
- 1
- 2
- 3
- 4
- 5
Mathematics for the Million: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Mathematics for the Million" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Mathematics for the Million — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Mathematics for the Million" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:

Notes on Using the Tables
I. IN TABLE I are given some of the more useful relations connecting weights and measures. In the metric system the units of length, weight, and capacity are the meter, gram, and liter. Each of these is sub-divided in the same way. A hundredth part has the prefix centi-, a thousandth part has the prefix milli-, and a thousand times has the prefix kilo-.
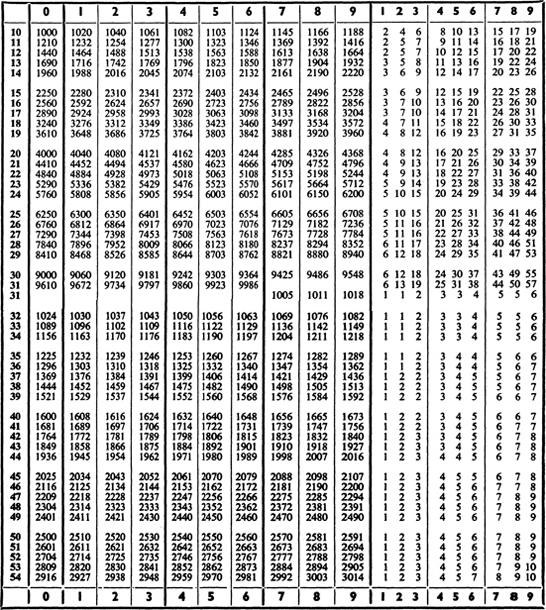
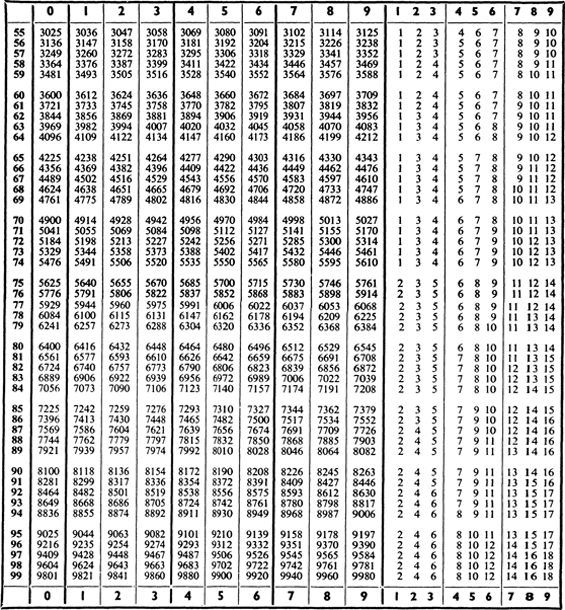
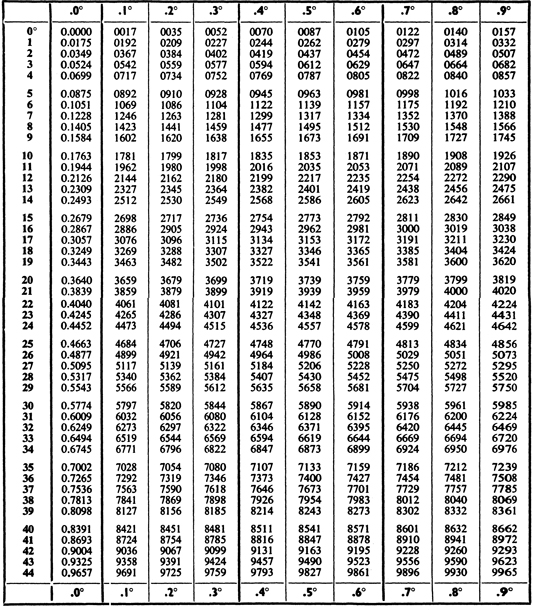
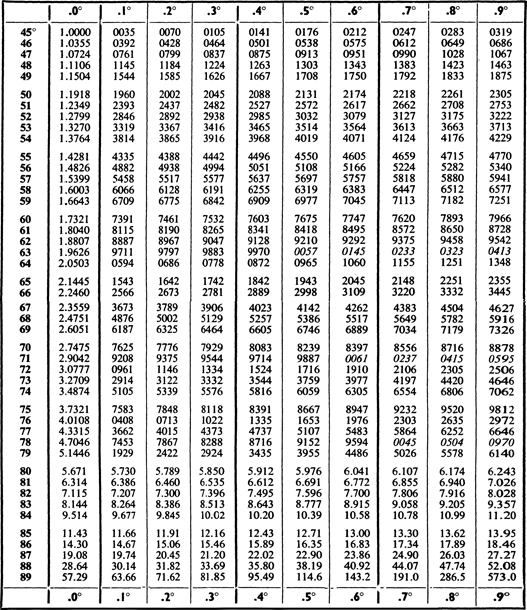
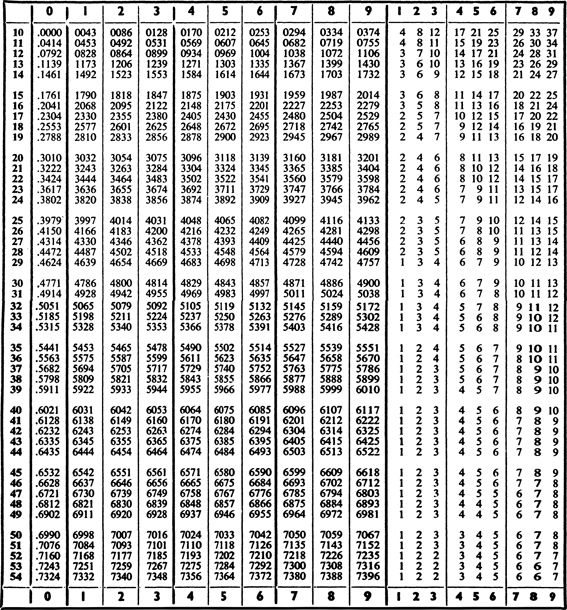
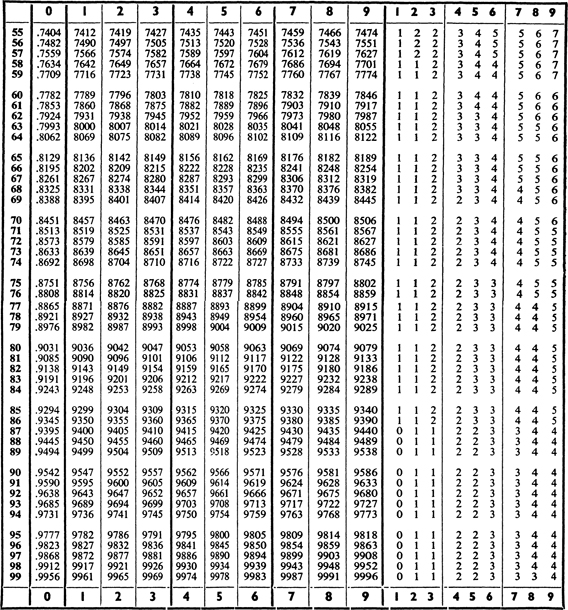
III. The use of the difference column has already been explained. Values between those shown in the difference column can be found by proportional parts. For example, we may want the square of 28.756. The table gives the square of 28.75 as 826.5. In this part of the difference column a difference of 1 in the number to be squared corresponds to a difference of 7 in the square. Therefore a difference of 0.6 will correspond approximately to a difference of 7 0.6, i.e., about 4. The square required is thus 826.9. Table III can also be used to find square roots. For example, we may want to find the square root of 123.2. By inspection we can see that the square root of this number lies between 11 and 12. In the tables we see that 1232 occurs twice, first corresponding to the digits 111, and then corresponding to the digits 351. The square root of 123.2 is thus 11.1. If we had wanted the square root of 12.32 it would clearly have been 3.51.
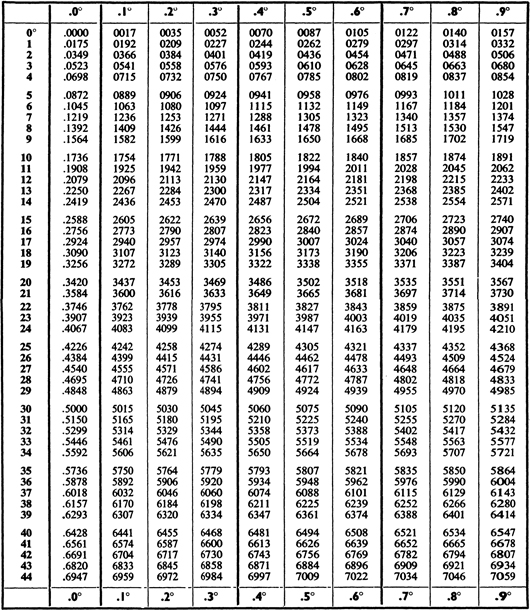
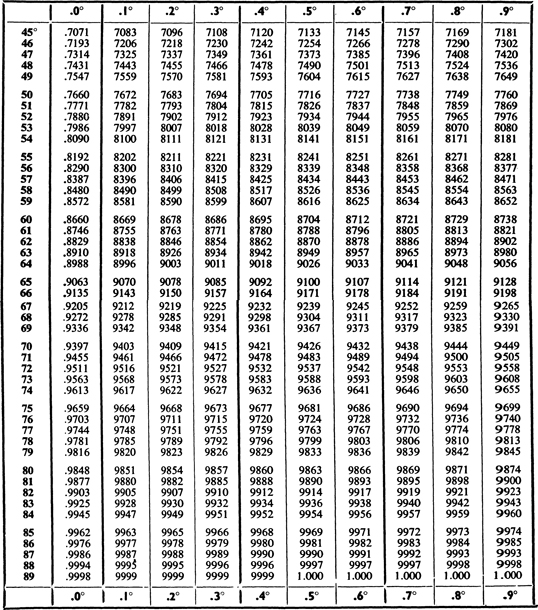
IV. In most tables of sines, etc., the parts of a degree are given in minutes, so that the steps are 6, 12, etc. The custom of expressing the steps as decimal fractions of a degree is, however, gradually being introduced.
The table of sines can also be used to find cosines by using the formula cos A = sin (90 A), e.g. to find cos 31.5, look up sin 58.5.
VI. A table of antilogarithms has been omitted for reasons of economy. Table VI can be used for finding numbers from their logarithms by simply reversing the process of finding the logarithm of a number. For directions for using the table see p. 449 and the note on Table III.
TABLE I
Weights and Measures
| 1,760 yards | = | 1 mile |
| 4,840 square yards | = | 1 acre |
| 640 acres | = | 1 square mile |
| 100 lbs. | = | 1 cwt. |
| 20 cwts. | = | 1 ton |
| 8 pints | = | 1 gallon |
| 1 gallon | = | 277 cubic inches |
| 1 cubic foot | = | 6.23 gallons |
Metric Weights and Measures
| 10 millimeters | = | 1 centimeter |
| 100 centimeters | = | 1 meter |
| 1,000 meters | = | 1 kilometer |
| l,000 grams | = | 1 kilogram |
| 100 centiliters | = | 1 liter |
| 1 liter | = | 1,000 cubic centimeters |
Metric Equivalents
| 1 inch | = | 2.54 centimeters |
| 1 lb. | = | 454 grams |
| 1 meter | = | 1.09 yards |
| 1 kilometer | = | 0.621 mile |
| 1 kilogram | = | 2.20 pounds |
| 1 liter | = | 0.22 gallon |
TABLE II
Constants
= 3.1416 log10 = 049.71
1 radian = 57.296 degrees
e = 2.7183 log10e = 0.4343
loge N = 2.3026 log10 N
log10 N = 0.4343 loge N
Earths mean radius = 3,960 miles = 6.371 108 centimeters
g = 32.2 feet per second per second, or 981 centimeters per second per second
1 cubic centimeter of water at 4 C. weighs 1 gram
WHEN ONE speaks of a branch of knowledge called mathematics at its most primitive level one signifies the existence of at least simple rules about calculation and measurement. The recognition of such rules presupposes that man has already at his disposal signs for numbers such as 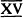 or 15, CXLVI or 146. To trace mathematics to its source we must therefore dig down to the primeval need for them. Most likely this was the impulse to keep track of the passage of time and, as such, to record the changing face of the heavens. For several millennia after mankind took this momentous step, star-lore was to be the pace-maker of mathematical ingenuity.
or 15, CXLVI or 146. To trace mathematics to its source we must therefore dig down to the primeval need for them. Most likely this was the impulse to keep track of the passage of time and, as such, to record the changing face of the heavens. For several millennia after mankind took this momentous step, star-lore was to be the pace-maker of mathematical ingenuity.
While our remote nomadic ancestors lived only by hunting and food gathering, the rising or setting position of stars on the horizon, whether they had or had not already risen when darkness fell and whether they had or had not yet done so at daybreak, were their only means of again locating a hunting ground already visited and their most reliable guide to the onset of the season at which particular game, berries, roots, eggs, shellfish, or grain would be most abundant at a particular location. As is true of all letterless communities today, members of our own species, while still nomads, must have realized that each star rises and sets a little earlier each day. They would date the routine of their joumeyings by the occasion when a particular star rose or set just before dawn, and rose or set just after sunset. Before there was farming of any sort, it is likely that the older folk of the tribe had learned to reckon in lunar time (i.e. successive full or new moons) when each boy and each girl would have reached the age for the tribal initiation ceremony.
At some time not much earlier than 10,000 BC and not later than 5000 BC settled village communities of herdsmen and grain growers came into being in the fertile regions of the Middle East. Here there was a larger leisure to observe the changing face of the night sky and a greater impetus to do so in the milieu of a seasonal timetable of lambing. sowing, and reaping. Here, too, there were more favourable conditions for observing the vagaries of the suns rising and setting positions and the varying length of its noon shadow from one rainy season to another. (See the photograph of Stonehenge in the illustrated section in the center of this book.)
Before 3000 BC, large concentrations of population with greater division of labour made their appearance on the banks of great rivers whose flooding annually enriched the nearby soil with fresh silt.
Such were the Nile of Egypt, in Iraq the Tigris and the Euphrates, the Indus in Pakistan, and farther east the Yangtse-Kiang and Hwang-ho. From the start in Egypt and in Iraq, we find a priestly caste responsible for the custody of a ceremonial calendar, equipped with writing of a sort including number signs, and housed in buildings placed to facilitate observations on celestial bodies as signposts of the calendar round. We may confidently conclude that the recognition of the year as a unit emerged in the village communities which coalesced to make these city-states and kingdoms. and that the recognition of a lunar month of 30 days preceded that of the Egyptian year of 365 days, i.e. 12 lunar months and 5 extra days. It began when the dog star Sirius was visible on the rim of the sky just before sunrise, an event portending the nearness of the annual flooding of the sacred river. Long before barter of cattle or sheep or produce of the soil began, man had experienced the need to count the passage of time and in doing so must have faced a challenge with which the counting of cattle in one and the same plot of land did not confront him imperatively. Pigs do not fly but time does. To count time in units of any sort we therefore need a tally to aid the memory. If for this reason only, it seems to be very likely that number signs take their origin from marks chipped on stone or wood to record successive days. Indeed, all the earliest batteries of number signs in use among the priestly astronomers responsible for the custody of the calendar disclose a repetition of strokes (Fig. 6). Of this there is more than a relic in the familiar Roman numerals: I, II, III, 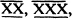
Font size:
Interval:
Bookmark:
Similar books «Mathematics for the Million»
Look at similar books to Mathematics for the Million. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book Mathematics for the Million and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.









