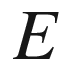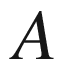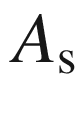Andreas chsner
Structural Mechanics with a Pen
A Guide to Solve Finite Difference Problems
1st ed. 2021
Logo of the publisher
Andreas chsner
Faculty of Mechanical Engineering, Esslingen University Applied Sciences, Esslingen am Neckar, Baden-Wrttemberg, Germany
ISBN 978-3-030-65891-5 e-ISBN 978-3-030-65892-2
https://doi.org/10.1007/978-3-030-65892-2
The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG 2021
This work is subject to copyright. All rights are solely and exclusively licensed by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed.
The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use.
The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, expressed or implied, with respect to the material contained herein or for any errors or omissions that may have been made. The publisher remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This Springer imprint is published by the registered company Springer Nature Switzerland AG
The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland
Preface
The classical approximation methods known in continuum mechanics are the finite difference method, the finite element method, the finite volume method, and the boundary element method. Each method has its advantages and disadvantages and a different spread in different areas of applied mechanics, e.g. solid or fluid mechanics. The oldest approximation method to solve partial differential equations is the finite difference method since the mathematical set of tools is basically limited to the series expansion of derivatives. More precisely, truncated Taylors series is used for the local expansions of the variables. This simple derivation of the method makes it quite attractive to introduce approximation methods in tertiary engineering education, e.g. in mechanical or civil engineering. This allows acquiring a general understanding of numerical approximation methods and the involved common steps such as discretization, assembly of a global system of equations, consideration of boundary and load conditions as well as the solution of a linear or nonlinear system of equations.
This book is focused on the introduction of the finite difference method based on the classical one-dimensional structural members, i.e. rods/bars and beams. It is the goal to provide a first introduction to the manifold aspects of the finite difference method and to enable the reader to get a methodical understanding of important subject areas in structural mechanics. The reader learns to understand the assumptions and derivations of different structural members. Furthermore, she/he learns to critically evaluate the possibilities and limitations of the finite difference method. Additional comprehensive mathematical descriptions, which solely result from advanced illustrations for two- or three-dimensional problems, are omitted. Hence, the mathematical description largely remains simple and clear.
Chapter introduces a simple treatment of elasto-plastic bending problems under the consideration of the thin beam formulation. The so-called layered approach is applied to linear-elastic/ideal-plastic material behavior and is restricted to monotonic loading.
All derivations in chapters two to four follow a common approach: based on the three basic equations of continuum mechanics, i.e. the kinematics relationship, the constitutive law, and the equilibrium equation, the partial differential equations, which describe the physical problem, are presented. The finite difference method is then used to derive approximate equations for the corresponding structural member.
In order to deepen the understanding of the derived equations and theories, each technical chapter collects at its end supplementary calculation problems. A short solution for each problem is included at the end of this book. It should be noted that these short solutions contain major steps for the solution of the problem and not only, for example, a numerical value for the final result. This should ensure that students are able to successfully master these problems. I hope that students find this book a useful complement to many classical textbooks. I look forward to receiving their comments and suggestions.
Andreas chsner
Esslingen, Germany
October 2020
Science knows no country, because knowledge belongs to humanity, and is the torch which illuminates the world.
Louis Pasteur (18221895)
Acknowledgements
It is important to highlight the contribution of the students which helped to develop the concept and content of this book. Their questions, comments, and struggles during difficult lectures, assignments, and final exams helped me to develop the idea for this approach. In addition, it is important to highlight the contribution of many undergraduate and postgraduate students. Furthermore, I would like to express my sincere appreciation to the Springer publisher, especially to Dr. Christoph Baumann, for giving me the opportunity to realize this book.
Symbols and Abbreviations
Latin Symbols (Capital Letters)
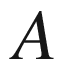
Area, cross-sectional area
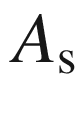
Shear area
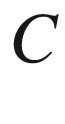
Elasticity constant
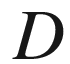
Bending rigidity

Compliance matrix