There are many reasons why neural networks fascinate us and have captivated headlines in recent years. They make web searches better, organize photos , and are even used in speech translation . Heck, they can even generate encryption . At the same time, they are also mysterious and mind-bending: how exactly do they accomplish these things ? What goes on inside a neural network?
On a high level, a network learns just like we do, through trial and error. This is true regardless if the network is supervised, unsupervised, or semi-supervised. Once we dig a bit deeper though, we discover that a handful of mathematical functions play a major role in the trial and error process. It also becomes clear that a grasp of the underlying mathematics helps clarify how a network learns.
In the following chapters we will unpack the mathematics that drive a neural network. To do this, we will use a feedforward network as our model and follow input as it moves through the network.
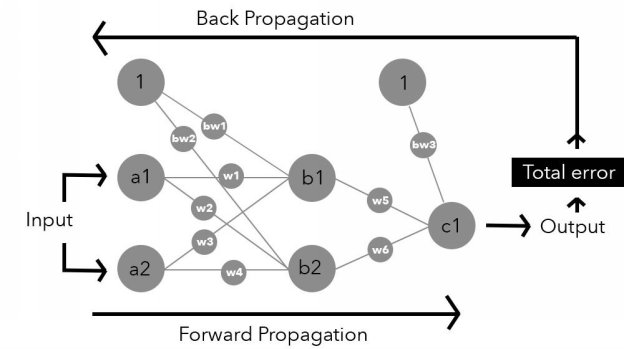
This "process" of moving through the network is complex though, so to make it easier and bite-size, we will divide it into 5 stages and take it slow.
Each of the stages includes at least one mathematical function, and we will devote an entire chapter to every stage. Our goal is that by the end, you will find neural networks less mind-bending and simply more fascinating. What's more, we hope that you'll be able to confidently explain these concepts to others and make use of them for yourself.
Here are the stages we will be exploring:
Required: Summation operator
Required: Activation function
Required: Cost function
Required: Partial derivative
Required: Chain Rule
Required: Gradient checking formula
Required: Weight update formula
However, before diving into the stages, we are going to clarify the terminology and notation that we will be using. We will also take a moment to build on the topics and ideas introduced in the previous chapters. Accomplishing these things will build up a solid framework and provide us with the tools required to move forward.
A extra few words before moving on:
You might be scratching your head and wondering if all networks have the same mathematical functions . The answer is a loud no , and for a few good reasons, including the network architecture, its purpose, and even the personal preferences of its developer. However, there is a general framework for feedforward models that includes a handful of mathematical functions, which is what we will be investigating.
On another note, the following chapters require a college-level grasp of algebra, statistics and calculus. A major concept you'll come across is calculating partial derivatives, which itself makes use of the chain rule. Please be aware of this! If you are rusty in these areas you might find yourself repeatedly frustrated. The Khan Academy offers top-notch free courses in algebra , calculus and statistics .
Terminology and Notation
If you are new to the field of neural networks or machine learning in general, one of the most confusing aspects can be the terminology and notation used. Textbooks, online lectures, and papers often vary in this regard.
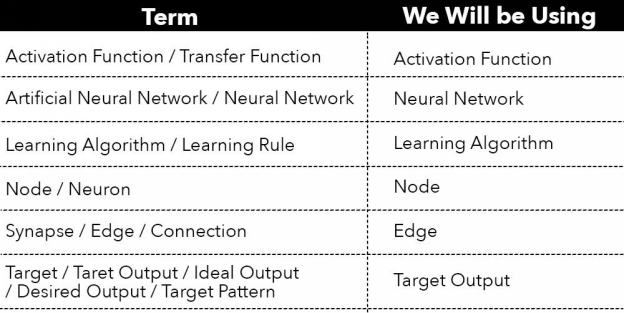
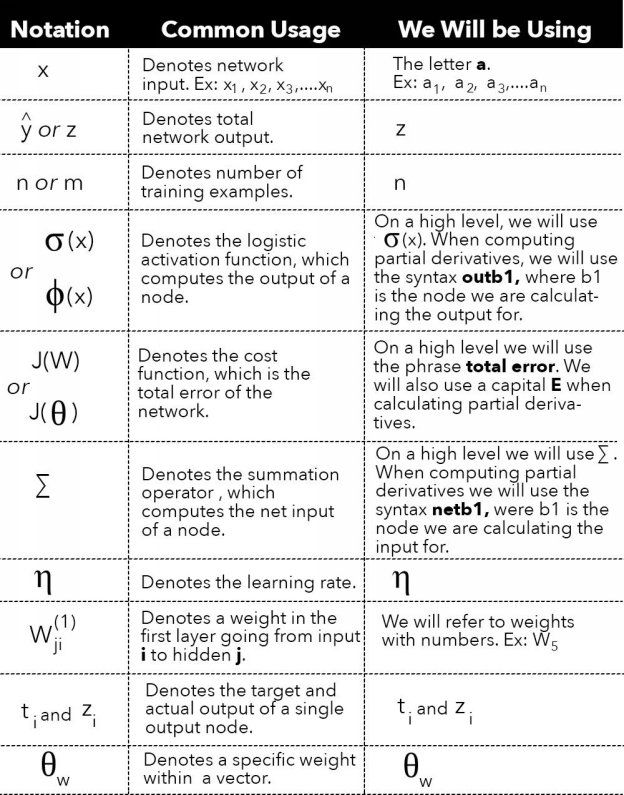
To help minimize potential frustration we have put together a few charts to explain what you can expect in this book.
The first is a list of common terms used to describe the same function, object or action, along with a clarification of which term we will be using. The second list contains common notation, along with a clarification of the notation we will be using. Hopefully this helps!
Note: The majority of these terms will be explained throughout each stage. However, you can always take a peek at our for additional help.
Terms:
The notation chart is on the next page. You might find it helpful to bookmark the page for reference.
Pre-Stage: Creating the Network Structure
There are many ways to construct a neural network, but all have a structure - or shell - that is made up of similar parts. These parts are called hyperparameters , and include elements such as the number of layers, nodes and the learning rate.
Hyperparameters are essentially fine tuning knobs that can be tweaked to help a network successfully train. In fact, they are determined before a network trains, and can only be adjusted manually by the individual or team who created the network. The network itself does not adjust them.


















