Britannica Educational Publishing - Geometry and Trigonometry

GEOMETRY AND TRIGONOMETRY

Published in 2015 by Britannica Educational Publishing (a trademark of Encyclopdia Britannica, Inc.) in association with The Rosen Publishing Group, Inc.

29 East 21st Street, New York, NY 10010

Copyright 2015 by Encyclopdia Britannica, Inc. Britannica, Encyclopdia Britannica, and the Thistle logo are registered trademarks of Encyclopdia Britannica, Inc. All rights reserved.

Rosen Publishing materials copyright 2015 The Rosen Publishing Group, Inc. All rights reserved.

Distributed exclusively by Rosen Publishing.

To see additional Britannica Educational Publishing titles, go to rosenpublishing.com.

First Edition

Britannica Educational Publishing

J. E. Luebering: Director, Core Reference Group

Anthony L. Green: Editor, Comptons by Britannica

Rosen Publishing

Hope Lourie Killcoyne: Executive Editor

Kathy Campbell: Editor

Nelson S: Art Director

Brian Garvey: Designer

Cindy Reiman: Photography Manager

Introduction and supplementary material by John Strazzabosco

Library of Congress Cataloging-in-Publication Data

Geometry and trigonometry/edited by James Stankowski.First edition.

pages cm.(The story of math, core principles of mathematics)

Includes bibliographical references and index.

ISBN 978-1-62275-528-8 (eBook)

1. Geometry. 2. Trigonometry. I. Stankowski, James, editor.

QA445.G474 2015

516--dc23

2014018167

Cover and interior pages iStockphoto.com/PashaIgnatov; cover (top), back cover, p. 3 (top) Indivision 07 Grow B/Getty Images.

Contents

T his book covers a broad collection of the principles of geometry and trigonometry inside a nice, compact format for the middle school and early high school student. Colorful diagrams bring the principles to life. The topics are enriched by references to famous mathematicians who discovered these principles and also snapshots of these principles at work in the real world. Seldom does a math book bring the story of so many topics in such a comprehensible way.

The student will find a wonderful resource that can always be consulted for quick help and location of ideas that arise even years later during formal math study and beyond.

Of course math discoveries are fascinating in themselves, and when they lead to wonderful, useful inventions, one sees why people study these ideas in the first place.

For instance, could a basic geometric shape be used to stop excruciating pain? Perhaps Euclid didnt have disease in mind when he began organizing the simplest of geometric figures, such as points, lines, and curves. But over the years other mathematicians took his shapes, and proved that certain geometric properties had qualities that today make people feel better, even if those individuals happen to be doubled over in pain from what are called kidney stones.

The particular geometrical shape required for medical healing in this case is called an ellipse, featured in this book. Inside the ellipse (or its three-dimensional relative, an egg shape or ellipsoid) is a point called a focus, near one end of the shape. Another focus appears near the other end of the shape. Scientists found that shooting sonar waves from one focus makes sounds that bounce off the inside walls of the ellipsoid, and they all strike the other focus at once, like a gentle hammer.

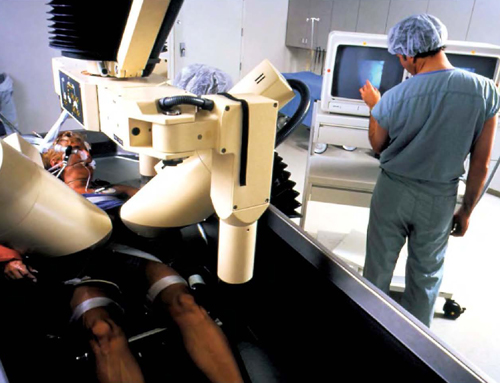
In lithotripsy, a lithotripter uses an ellipsoid and a focus point to send sound waves to shatter a patients gallstones or kidney stones into miniscule pieces. Southern Illinois University/Photo Researchers/Getty Images

Thats how doctors use those sounds, special instruments (such as a lithotripter machine), and ellipsoids to help break up kidney stones in the patient. No surgery is needed. The patient makes a faster recovery than if surgery had been used. His or her kidney stones are painlessly shattered with no harm to the kidney, and the patient might go to school or work the very next day.

When readers enter the pages of this book and see the basics of geometry and trigonometry, it pays to ask themselves with each figure they see, could they discover some great invention with this shape? Could they save lives? Could they ease pain? Could they somehow use it to create a new invention? What problem might they solve with it?

Students will discover why trigonometry is called that, and theyll see a math topic begin to unfold that, strangely, they have already used quite a bit even though they might not have been aware of it. Trigonometry is embedded in the software of computers. When people have played a computer game where their car, for instance, spins and misses trouble on the road, the joystick is really telling the computer to use trigonometry formulas to get the car to do what the players want. So the math comes alive for these individuals. Theyll encounter in this book some basics of trigonometry, often fondly called trig.

Finally, readers will also find fascinating information on great mathematicians who made the ideas of geometry and trigonometry apply to wonderful discoveries that have changed the world they live in.

T he ancient branch of mathematics known as geometry deals with points, lines, surfaces, and solidsand their relationships. In particular, geometry may be thought of as offering (1) precise definitions of many different figures; (2) construction methods for drawing figures; (3) a wealth of facts about the figures; and, most important, (4) ways to prove the facts.

Geometry was thoroughly organized in about 300 BCE , when the Greek mathematician Euclid gathered what was known at the time, added original work of his own, and arranged 465 propositions into 13 books, collectively called Elements. The books covered not only plane and solid geometry but also much of what is now known as algebra, trigonometry, and advanced arithmetic.

Down through the ages, the propositions have been rearranged, and many of the proofs are different, but the basic idea presented in the Elements has not changed. In the work, facts are not just cataloged but are developed in an orderly way, starting with statements (definitions, common notions, and postulates) that seem perfectly self-evident, with each successive theorem proved by using only previously shown facts. This mode of reasoning, known as the axiomatic method, has profoundly influenced epistemology (the study of the nature, origin, and limits of human knowledge) and education.

Even in 300 BCE , geometry was recognized to be not just for mathematicians. Anyone can benefit from the basic teachings of geometry, which are how to follow lines of reasoning, how to say precisely what is intended, and especially how to prove basic concepts by following these lines of reasoning. Taking a course in geometry is beneficial for all students, who will find that learning to reason and prove convincingly is necessary for every profession. It is true that not everyone must prove things, but everyone is exposed to proof. Politicians, advertisers, and many other people try to offer convincing arguments. Anyone who cannot tell a good proof from a bad one may easily be persuaded in the wrong direction. Geometry provides a simplified universe, where points and lines obey believable rules and where conclusions are easily verified. By first studying how to reason in this simplified universe, people can eventually, through practice and experience, learn how to reason in a complicated world.