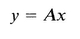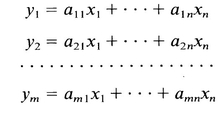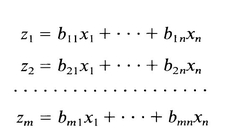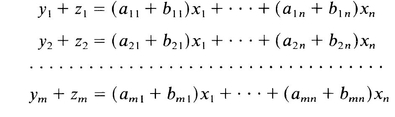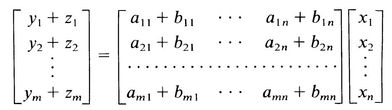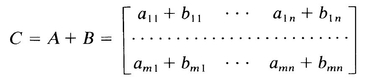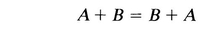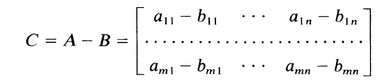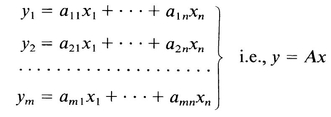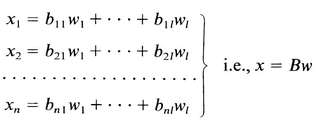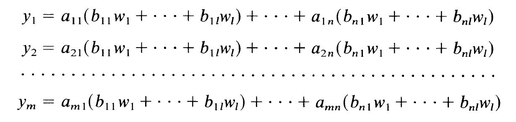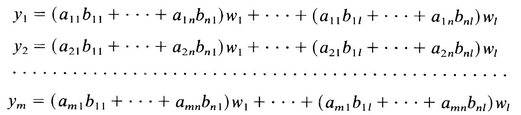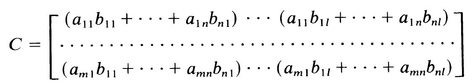Bernard Friedland - Control System Design

Consider a system of linear equations

(A.1)

To reduce the amount of writing, (A.1 ) can be expressed as

(A.2)

The arrays of numbers enclosed by the square brackets are known as matrices. In general a rectangular array having m columns and n rows, of the form

(A.3)

is called an n m matrix. A single letter A is used to designate the entire n m matrix. The matrices in (A.2) having only one column, namely

(A.4)

are generally called vectors . (The three-dimensional vectors of classical physics are special cases of the general mathematical vectors used in this book. When, as in Chap. 3, we want to refer specifically to a physical vector such as force or velocity, we use an arrow over the letter, viz., )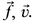

Since a vector is a 1 n matrix, any result that applies to all n m matrices also applies to vectors. As is customary in texts on systems, vectors are generally denoted by lowercase letters and other matrices are generally denoted by capital letters.

In terms of the notation introduced above, the system of linear equations (A.1) can be written simply as

(A.5)

Equation (A.5) can be read as (the vector) y is the result of multiplying (the vector) x by (the matrix) A . Thus we have defined the operation of multiplying a vector by a matrix, as the equivalent of the system of linear equations (A.1). Multiplying a vector by a matrix is a special case of multiplying one matrix by another. We shall consider this operation and others in the next section.

A 1 x 1 matrix (i.e., a single component vector) which is just a single number, is known as a scalar .

To save writing, the matrix A is sometimes exhibited as

A = [ a ij ]

where a ij is a typical element of the matrix A.

A.3 MATRIX OPERATIONS

Addition and subtraction Matrices can be combined by use of the operations of addition, subtraction, and multiplication in much the same manner as scalars. These operations may be defined in terms of systems of simultaneous equations. Thus, suppose

(A.6)

and

(A.7)

then, adding each equation in (A.6) to the corresponding equation in (A.7) gives

or, in the matrix shorthand,

or

y + z = (A + B)x = Cx

where

(A.8)

Thus each term in the sum of two matrices is the sum of the corresponding elements of the summands. It is clear from the definition that two matrices can be added only when they are both of the same dimensions: m n , and, when A + B is defined,

(A.9)

Subtraction of two matrices is defined by

(A.10)

Multiplication Multiplication of matrices is defined in terms of substitution of one linear system of equations into another. Consider

(A.11)

and

(A.12)

Substitute (A.11) into (A.12) to obtain

(A.13)

Collecting coefficients of the wi in (A.13) gives

(A.14)

or

where

(A.15)

Now, since in shorthand notation (A.11) and (A.12) are

y = Ax and x = Bw

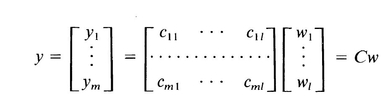
we can write

y = A ( Bw ) = ABw = Cw

where C is the product matrix defined by (A.15). In words, the ( i , j )th element c ij of the product matrix is computed by multiplying and summing the elements of the ith row of the first matrix A by the j th column of the second matrix B :
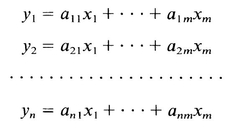
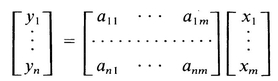
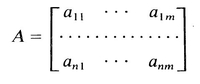
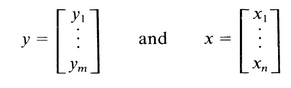