Paul Lockhart - Measurement

MEASUREMENT

PAUL LOCKHART

THE BELKNAP PRESS OF HARVARD UNIVERSITY PRESS

CAMBRIDGE, MASSACHUSETTS LONDON, ENGLAND

2012

Copyright 2012 by the President and Fellows of Harvard College

All rights reserved

Jacket designer: Tim Jones

Jacket art: Artwork by Sanzio Raffaello, 15th century, ink, courtesy of Photoservice Electa/Getty Images

Library of Congress Cataloging-in-Publication Data

Lockhart, Paul.

Measurement / Paul Lockhart.

p. cm.

Includes index.

ISBN 978-0-674-05755-5 (hardcover : alk. paper)

1. Geometry. I. Title.

QA447.L625 2012

516dc23 2012007726

For Will, Ben, and Yarrow

In which we begin our investigation of abstract geometrical figures. Symmetrical tiling and angle measurement. Scaling and proportion. Length, area, and volume. The method of exhaustion and its consequences. Polygons and trigonometry. Conic sections and projective geometry. Mechanical curves.

Containing some thoughts on mathematical motion. Coordinate systems and dimension. Motion as a numerical relationship. Vector representation and mechanical relativity. The measurement of velocity. The differential calculus and its myriad uses. Some final words of encouragement to the reader.

There are many realities out there. There is, of course, the physical reality we find ourselves in. Then there are those imaginary universes that resemble physical reality very closely, such as the one where everything is exactly the same except I didnt pee in my pants in fifth grade, or the one where that beautiful dark-haired girl on the bus turned to me and we started talking and ended up falling in love. There are plenty of those kinds of imaginary realities, believe me. But thats neither here nor there.

I want to talk about a different sort of place. Im going to call it mathematical reality. In my minds eye, there is a universe where beautiful shapes and patterns float by and do curious and surprising things that keep me amused and entertained. Its an amazing place, and I really love it.

The thing is, physical reality is a disaster. Its way too complicated, and nothing is at all what it appears to be. Objects expand and contract with temperature, atoms fly on and off. In particular, nothing can truly be measured. A blade of grass has no actual length. Any measurement made in this universe is necessarily a rough approximation. Its not bad; its just the nature of the place. The smallest speck is not a point, and the thinnest wire is not a line.

Mathematical reality, on the other hand, is imaginary. It can be as simple and pretty as I want it to be. I get to have all those perfect things I cant have in real life. I will never hold a circle in my hand, but I can hold one in my mind. And I can measure it. Mathematical reality is a beautiful wonderland of my own creation, and I can explore it and think about it and talk about it with my friends.

Now, there are lots of reasons people get interested in physical reality. Astronomers, biologists, chemists, and all the rest are trying to figure out how it works, to describe it.

I want to describe mathematical reality. To make patterns. To figure out how they work. Thats what mathematicians like me try to do.

The point is I get to have them bothphysical reality and mathematical reality. Both are beautiful and interesting (and somewhat frightening). The former is important to me because I am in it, the latter because it is in me. I get to have both these wonderful things in my life and so do you.

My idea with this book is that we will design patterns. Well make patterns of shape and motion, and then we will try to understand our patterns and measure them. And we will see beautiful things!

But I wont lie to you: this is going to be very hard work. Mathematical reality is an infinite jungle full of enchanting mysteries, but the jungle does not give up its secrets easily. Be prepared to struggle, both intellectually and creatively. The truth is, I dont know of any human activity as demanding of ones imagination, intuition, and ingenuity. But I do it anyway. I do it because I love it and because I cant help it. Once youve been to the jungle, you can never really leave. It haunts your waking dreams.

So I invite you to go on an amazing adventure! And of course, I want you to love the jungle and to fall under its spell. What Ive tried to do in this book is to express how math feels to me and to show you a few of our most beautiful and exciting discoveries. Dont expect any footnotes or references or anything scholarly like that. This is personal. I just hope I can manage to convey these deep and fascinating ideas in a way that is comprehensible and fun.

Still, expect it to be slow going. I have no desire to baby you or to protect you from the truth, and Im not going to apologize for how hard it is. Let it take hours or even days for a new idea to sink init may have originally taken centuries!

Im going to assume that you love beautiful things and are curious to learn about them. The only things you will need on this journey are common sense and simple human curiosity. So relax. Art is to be enjoyed, and this is an art book. Math is not a race or a contest; its just you playing with your own imagination. Have a wonderful time!

What is a math problem? To a mathematician, a problem is a probea test of mathematical reality to see how it behaves. It is our way of poking it with a stick and seeing what happens. We have a piece of mathematical reality, which may be a configuration of shapes, a number pattern, or what have you, and we want to understand what makes it tick: What does it do and why does it do it? So we poke itonly not with our hands and not with a stick. We have to poke it with our minds.

As an example, lets say youve been playing around with triangles, chopping them up into other triangles and so forth, and you happen to make a discovery:

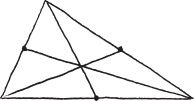
When you connect each corner of a triangle to the middle of the opposite side, the three lines seem to all meet at a point. You try this for a wide variety of triangles, and it always seems to happen. Now you have a mystery! But lets be very clear about exactly what the mystery is. Its not about your drawings or what looks like is happening on paper. The question of what pencil-and-paper triangles may or may not do is a scientific one about physical reality. If your drawing is sloppy, for example, then the lines wont meet. I suppose you could make an extremely careful drawing and put it under a microscope, but you would learn a lot more about graphite and paper fibers than you would about triangles.

The real mystery is about imaginary, too-perfect-to-exist triangles, and the question is whether these three perfect lines meet in a perfect point in mathematical reality. No pencils or microscopes will help you now. (This is a distinction I will be stressing throughout the book, probably to the point of annoyance.) So how are we to address such a question? Can anything ever really be known about such imaginary objects? What form could such knowledge take?

Before examining these issues, lets take a moment to simply delight in the question itself and to appreciate what is being said here about the nature of mathematical reality.

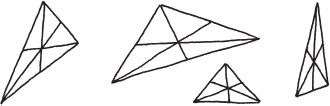
What weve stumbled onto is a conspiracy. Apparently, there is some underlying (and as yet unknown) structural interplay going on that is making this happen. I think that is marvelous and also a little scary. What do triangles know that we dont? Sometimes it makes me a little queasy to think about all the beautiful and profound truths out there waiting to be discovered and connected together.