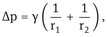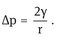1.1 Definition of the interfacial region and interfacial tension
.
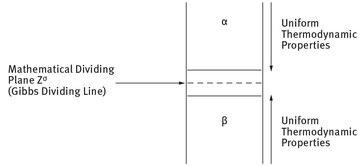
: The Gibbs dividing line.
Using Gibbs model, it is possible to obtain a definition of the surface or interfacial tension . The surface free energy dG is made of three components: an entropy term, SdT; an interfacial energy term, Ad; a composition term nidi (ni is the number of moles of component i with chemical potential i).
The GibbsDeuhem equation is,
At constant temperature and composition,
For a stable interface is positive, i.e. if the interfacial area increases, G increases. Note that is energy per unit area (mJm2) which is dimensionally equivalent to force per unit length (mNm1), the unit usually used to define surface or interfacial tension.
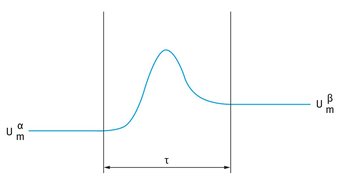
An alternative approach to Gibbs treatment was given by Guggenheim [2] in which two dividing planes are drawn, one in phase , the other in phase , as is illustrated in .
: Guggenheim convention of the interfacial region.
The planes are sufficiently far outside the interfacial region that beyond them the two phases have their bulk properties with internal energy 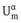 and
and 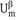 . In this convention the interfacial region is enclosed between two planes, a distance apart. The interfacial region has now a finite volume A. In this convention the value of excess quantities depends on the choice of the two planes and hence on , whereas in the Gibbs convention it depends on the choice of one location of the dividing plane. The Guggenheim analysis [2] for the interfacial region is quite complex and hence the more simple Gibbs convention [1] is used in the analysis of interfacial phenomena.
. In this convention the interfacial region is enclosed between two planes, a distance apart. The interfacial region has now a finite volume A. In this convention the value of excess quantities depends on the choice of the two planes and hence on , whereas in the Gibbs convention it depends on the choice of one location of the dividing plane. The Guggenheim analysis [2] for the interfacial region is quite complex and hence the more simple Gibbs convention [1] is used in the analysis of interfacial phenomena.
For a curved interface, one should consider the effect of the radius of curvature. Fortunately, for a curved interface is estimated to be very close to that of a planer surface, unless the droplets are very small (< 10 nm).
Curved interfaces produce some other important physical phenomena which affect emulsion properties, e.g. the Laplace pressure p which is determined by the radii of curvature of the droplets,
where r1 and r2 are the two principal radii of curvature.
For a perfectly spherical droplet r1 = r2 = r and
For a hydrocarbon droplet with radius 100 nm, and = 50 mNm1, p 106 Pa ( 10 atm).
1.2 Role of interfacial phenomena
In all disperse systems such as suspensions, emulsions, foams, etc., the structure of the interfacial region determines its colloidal properties [36]. The larger the interfacial area, i.e. the larger the surface to volume ratio of the particle or droplet, the more important the role of the structure of the interfacial region. The colloid stability /instability of any disperse system is determined by the property of the interfacial region. In actual fact colloid and interface science are one individual subject. This is particularly the case with charged interfaces that form electrical double layers and those interfaces that contain adsorbed surfactants and/or polymers. With systems containing electrical double layers, repulsion between the particles or droplets takes place as a result of the overlap of double layers. This is particularly the case at low electrolyte concentrations and low valency of the indifferent electrolyte. This double layer repulsion overcomes the van der Waals attraction and at intermediate distances an energy barrier is produced that prevents approach of the particles. This barrier can reach several kT units (where k is the Boltzmann constant and T is the absolute temperature) which becomes much higher than the thermal motion ( kT) and this prevents particle aggregation (flocculation or coagulation). As the electrolyte concentration is increased, the range and magnitude of the repulsive energy is reduced and at a critical concentration (defined as the critical coagulation concentration, ccc) fast flocculation and irreversible aggregation occur. With adsorbed nonionic surfactants or polymers an adsorbed layer with thickness is produced. When the particles or droplets approach a surface-surface distance h < 2, strong repulsion occurs due to the unfavorable mixing of the adsorbed chains when these are in good solvent conditions. This repulsion is referred to as steric interaction and at distances < 2 a very sharp increase in repulsion energy occurs when h < 2. This steric repulsion overcomes the van der Waals attraction at h 2. The repulsion produced by the presence of adsorbed layers of surfactant or polymers is generally more effective than the electrostatic repulsion produced by overlap of the double layers. The stability is less sensitive to addition of moderate electrolyte concentration, provided the medium remains a good solvent for the chains.













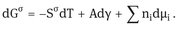
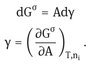
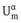 and
and 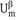 . In this convention the interfacial region is enclosed between two planes, a distance apart. The interfacial region has now a finite volume A. In this convention the value of excess quantities depends on the choice of the two planes and hence on , whereas in the Gibbs convention it depends on the choice of one location of the dividing plane. The Guggenheim analysis [2] for the interfacial region is quite complex and hence the more simple Gibbs convention [1] is used in the analysis of interfacial phenomena.
. In this convention the interfacial region is enclosed between two planes, a distance apart. The interfacial region has now a finite volume A. In this convention the value of excess quantities depends on the choice of the two planes and hence on , whereas in the Gibbs convention it depends on the choice of one location of the dividing plane. The Guggenheim analysis [2] for the interfacial region is quite complex and hence the more simple Gibbs convention [1] is used in the analysis of interfacial phenomena.