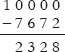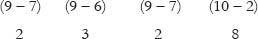Gupta - The Power of Vedic Maths with Trigonometry
Here you can read online Gupta - The Power of Vedic Maths with Trigonometry full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2005, publisher: Jaico Publishing House, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
The Power of Vedic Maths with Trigonometry: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "The Power of Vedic Maths with Trigonometry" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
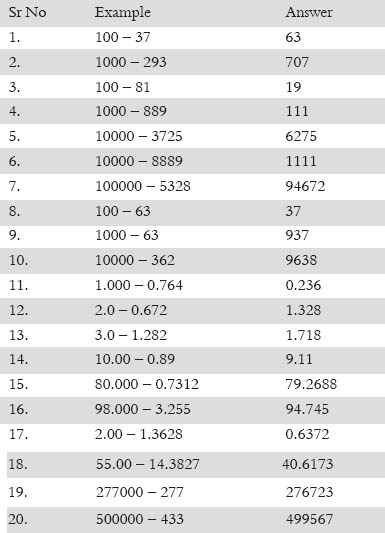
Vedic Maths, as the name suggests, has originated from the Vedas. It consists of using 16 sutras, that simplify math to a level where students can solve problems mentally. Most calculations are only a line long, thus answers are easy and quick to find! The Power of Vedic Maths 1st Edition brings together unique methods that solve problems of algebra, arithmetic, trigonometry, calculus, and coordinate geometry.
The author has skillfully used a step-by-step approach to explain basic concepts of this system to the readers. This easy-to-understand guide, shows the applications of Vedic maths in the contemporary world. The Power of Vedic Maths 1st Edition can be of great help to students preparing for competitive examinations like CET, AIEEE, and CAT. The guide is lined with many solved problems, and has 1000 practice questions for students to solve for themselves. Vedic math techniques can go a long way in significantly reducing the time taken to calculate answers. This boosts self confidence, and leads students enjoy mathematics instead of fearing it. Some techniques covered in the book focus on multiplication, division, computation of squares and square roots, and complex fractions. The Power of Vedic Maths 1st Edition also has a special chapter that shows how to solve problems that have previously appeared in competitive exams.
The Power of Vedic Maths is not restricted to only students. The methods stated in the book can be used to solve mathematical calculations that people face in their daily lives. The fundamentals can be put to practice by anyone willing to try Vedic math, including parents, teachers, and people with non-mathematical backgrounds. Infact, the popularity of this mathematics system is increasing rapidly as people are implementing the concepts in real life.
The Power of Vedic Maths is a great way to learn an Indian system that is thousands of years old, and yet extremely relevant in today s world
Gupta: author's other books
Who wrote The Power of Vedic Maths with Trigonometry? Find out the surname, the name of the author of the book and a list of all author's works by series.