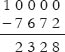Gupta - The power of Vedic maths: for admission tests, professional & competitive examinations

THE POWER OF

VEDIC
MATHS

2nd EDITION

ATUL GUPTA

Published by Jaico Publishing House

A-2 Jash Chambers, 7-A Sir Phirozshah Mehta Road

Fort, Mumbai - 400 001

www.jaicobooks.com

Atul Gupta

THE POWER OF VEDIC MATHS

ISBN 81-7992-357-6

First Jaico Impression: 2004

Thirteenth Jaico Impression (Revised & Updated): 2010

Fifteenth Jaico Impression: 2011

No part of this book may be reproduced or utilized in any form or by any means, electronic or mechanical including photocopying, recording or by any information storage and retrieval system, without permission in writing from the publishers.

Contents

PREFACE

Mathematics is considered to be a dry and boring subject by a large number of people. Children dislike and fear mathematics for a variety of reasons. This book is written with the sole purpose of helping school and college students, teachers, parents, common people and people from non-mathematical areas of study, to discover the joys of solving mathematical problems by a wonderful set of techniques called Vedic Maths.

These techniques are derived from 16 sutras (verses) in the Vedas, which are thousands of years old and among the earliest literature of ancient Hindus in India. They are an endless source of knowledge and wisdom, providing practical knowledge in all spheres of life. Jagadguru Swami Sri Bharati Krshna Tirthaji (1884-1960) was a brilliant scholar who discovered the 16 sutras in the Vedas and spent 8 years in their intense study. He has left an invaluable treasure for all generations to come, consisting of a set of unique and magnificent methods for solving mathematical problems in areas like arithmetic, algebra, calculus, trigonometry and co-ordinate geometry. These techniques are very easy to learn and encapsulate the immense and brilliant mathematical knowledge of ancient Indians, who had made fundamental contributions to mathematics in the form of the decimal numerals, zero and infinity.

I have trained thousands of children of all age groups with these techniques and I find that even young children enjoy learning and using them. The techniques reduce drastically, the number of steps required to solve problems and in many cases, after a little practice, many of the problems can be solved orally. It gives tremendous self-confidence to the students which leads them to enjoy mathematics instead of fearing and disliking it.

I have written this book in the form of a cookbook, where a reader can grasp a technique quickly, instead of reading through a large mass of theory before understanding it. I have considered techniques for major arithmetical operations like multiplication, division, computation of squares and square roots and complex fractions, besides a whole lot of other techniques. Each technique has been explained in detail with the help of solved examples, using a step-by-step approach and I am sure that the reader will be able to understand and master the contents easily. Every chapter has a large number of problems for practice and the book contains over 1000 such problems. The answers are given alongside so that the reader can either solve the problems orally or use paper and pen and compare with the given answer. The chapters should be read sequentially to absorb the material and then can be used for reference in any desired order.

I have also included a special chapter in which I have shown the application of the techniques to solve problems, collected from several competitive exams. This is a unique feature of the book and should add to the popularity of the techniques.

I have tried to make all the examples and answers error-free but if any mistake is discovered, I will be obliged if I am informed about the same.

Constructive criticism and comments can be sent to me at

ATUL GUPTA

Mobile: 9820845036

TWO SIMPLE TECHNIQUES

We will begin our journey into the fascinating world of Vedic maths with two simple techniques which will lay the foundation for some of the techniques in the following chapters.

I. Subtraction from 100/1000/10000

We will start with a very simple technique wherein we will see the use of the sutra All from 9 and last from 10. This is used to subtract a given number from 100, 1000, 10000 etc. It removes the mental strain which is existent in the method taught in schools.

This method is also used later on in the Nikhilam method of multiplication.

Consider the subtraction of 7672 from 10000.

a) Normal Method

The normal method is

We carry 1 from the left side and continue doing so till we reach the rightmost digit, leaving behind 9 in each column and 10 in the last column.

Then, we subtract the right most digit 2 from 10 and write down 8. Next, we subtract the digit 7 from 9 and write down 2.

We repeat this process for all the remaining digits to the left.

Through this operation, the final result is always obtained from right to left.

Mentally, there is a carry operation for every digit, which is time consuming and slows down the overall process.

b) Vedic Method

The Vedic method uses the sutra All from 9 and last from 10 and gives a very simple and powerful technique to achieve the same result.

The result can be obtained from both left to right as well as right to left with equal ease. It states that the result can be obtained by subtraction of each digit from 9 and the last digit from 10.

Hence, in the given example,

We can get the result from left to right or vice versa from right to left as

i.e. all digits except the last one are subtracted from 9, the last digit is subtracted from 10 and the result (2328) is written down directly. The mental burden of a carry for each column vanishes and the answer can be obtained easily, in a jiffy.

The same technique can be applied for decimal subtraction also, e.g. 2.000 - 0.3436.

The core operation here is subtraction of 3436 from 10000 where 1 is a carry from left.

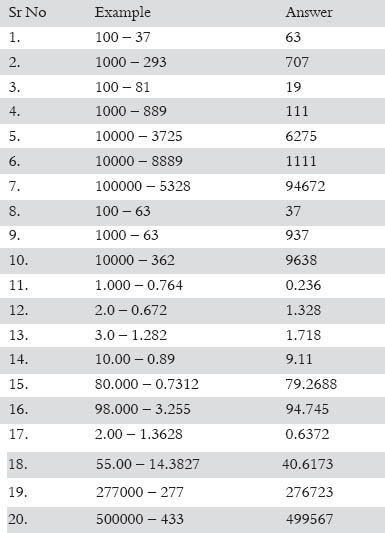
1. Examples for subtractions from bases of 100, 1000 etc.

This simple subtraction method will be used further in multiplication ().

II. Multiplication with a series of 9s

a) Multiplication of a number by same number of 9s

Let us use this technique to see how to carry out multiplication of an n-digit number by a number with n number of 9s eg. any 3-digit number by 999 or a 4-digit number by 9999.

Let us see an example viz. 533 999

The solution can be obtained as 533 (1000 - 1)

= 533000 - 533