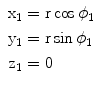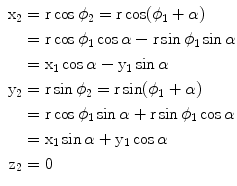In the usual crystallographic sense, symmetry operations are defined as rotations and reflections that turn a body into a congruent position. This can be realized in two ways. The active view of a rotation is the following. An observer takes a snapshot of a crystal, then the crystal is rotated while the camera is left immobile. A second snapshot is taken. If the two snapshots are identical, then we have performed a symmetry operation. In the passive view, the camera takes a snapshot of the crystal, then the camera is displaced while the crystal is left immobile. From a new perspective a second snapshot is taken. If this is the same as the first one, we have found a symmetry-related position. Both points of view are equivalent as far as the relative positions of the observer and the crystal are concerned. However, viewed in the frame of absolute space, there is an important difference: if the rotation of the crystal in the active view is taken to be counterclockwise, the rotation of the observer in the passive alternative will be clockwise. Hence, the transformation from active to passive involves a change of the sign of the rotation angle. In order to avoid annoying sign problems, only one choice of definition should be adhered to. In the present monograph we shall consistently adopt the active view , in line with the usual convention in chemistry textbooks. In this script the part of the observer is played by the set of coordinate axes that defines the absolute space in a Cartesian way. They will stay where they are. On the other hand, the structures, which are operated on, are moving on the scene. To be precise, a symmetry operation
will move a point P 1 with coordinates (x1,y1,z1) to a new position P 2 with coordinates (x2,y2,z2):
A pure rotation,
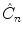
( n >1), around a given axis through an angle 2/ n radians displaces all the points, except the ones that are lying on the rotation axis itself. A reflection plane,
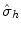
, moves all points except the ones lying in the reflection plane itself. A rotationreflection,
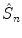
( n >2), is a combination in either order of a
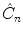
rotation and a reflection through a plane perpendicular to the rotation axis. As a result, only the point of intersection of the plane with the axis perpendicular to it is kept. A special case arises for n =2. The
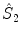
operator corresponds to the inversion and will be denoted as
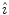
. It maps every point onto its antipode. A plane of symmetry can also be expressed as the result of a rotation through an angle around an axis perpendicular to the plane, followed by inversion through the intersection point of the axis and the plane. A convenient way to present these operations is shown in Fig.. Operator products are right-justified, so that
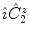
means that
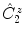
is applied first, and then the inversion acts on the intermediate result:
Fig. 1.1
Stereographic view of the reflection plane. The point P 1, indicated by X, is above the plane of the gray disc. The reflection operation in the horizontal plane,
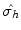
, is the result of the
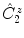
rotation around the center by an angle of , followed by inversion through the center of the diagram, to reach the position P 3 below the plane, indicated by the small circle
From the mathematical point of view the rotation of a point corresponds to a transformation of its coordinates. Consider a right-handed Cartesian coordinate frame and a point P 1 lying in the xy plane. The point is being subjected to a rotation about the upright z -axis by an angle . By convention, a positive value of will correspond to a counterclockwise direction of rotation. An observer on the pole of the rotation axis and looking down onto the plane will view this rotation as going in the opposite sense to that of the rotation of the hands on his watch. A synonym for counterclockwise here is right-handed. If the reader orients his/her thumb in the direction of the rotational pole, the palm of his/her right hand will indicate the counterclockwise direction. The transformation can be obtained as follows. Let r be the length of the radius-vector, r , from the origin to the point P 1, and let 1 be the angular coordinate of the point measured in the horizontal plane starting from the x -direction, as shown in Fig.. The coordinates of P 1 are then given by
Rotating the point will not change its distance from the origin, but the angular coordinate will increase by . The angular coordinate of P 2 will thus be given by 2= 1+. The coordinates of the image point in terms of the coordinates of the original point are thus given by
In this way the coordinates of P 2 are obtained as functions of the coordinates of P 1 and the rotation angle. This derivation depends simply on the trigonometric relationships for sums and differences of angles. We may also express this result in the form of a matrix transformation. For this, we put the coordinates in a column vector and operate on it (on the left) by means of a transformation matrix
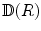













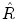 will move a point P 1 with coordinates (x1,y1,z1) to a new position P 2 with coordinates (x2,y2,z2):
will move a point P 1 with coordinates (x1,y1,z1) to a new position P 2 with coordinates (x2,y2,z2): 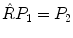
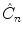 ( n >1), around a given axis through an angle 2/ n radians displaces all the points, except the ones that are lying on the rotation axis itself. A reflection plane,
( n >1), around a given axis through an angle 2/ n radians displaces all the points, except the ones that are lying on the rotation axis itself. A reflection plane, 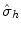 , moves all points except the ones lying in the reflection plane itself. A rotationreflection,
, moves all points except the ones lying in the reflection plane itself. A rotationreflection, 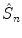 ( n >2), is a combination in either order of a
( n >2), is a combination in either order of a 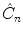 rotation and a reflection through a plane perpendicular to the rotation axis. As a result, only the point of intersection of the plane with the axis perpendicular to it is kept. A special case arises for n =2. The
rotation and a reflection through a plane perpendicular to the rotation axis. As a result, only the point of intersection of the plane with the axis perpendicular to it is kept. A special case arises for n =2. The 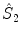 operator corresponds to the inversion and will be denoted as
operator corresponds to the inversion and will be denoted as 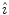 . It maps every point onto its antipode. A plane of symmetry can also be expressed as the result of a rotation through an angle around an axis perpendicular to the plane, followed by inversion through the intersection point of the axis and the plane. A convenient way to present these operations is shown in Fig.. Operator products are right-justified, so that
. It maps every point onto its antipode. A plane of symmetry can also be expressed as the result of a rotation through an angle around an axis perpendicular to the plane, followed by inversion through the intersection point of the axis and the plane. A convenient way to present these operations is shown in Fig.. Operator products are right-justified, so that 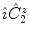 means that
means that 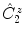 is applied first, and then the inversion acts on the intermediate result:
is applied first, and then the inversion acts on the intermediate result: 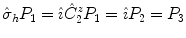
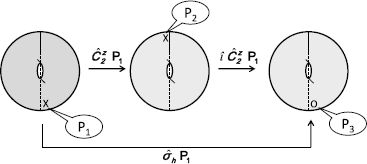
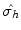 , is the result of the
, is the result of the 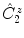 rotation around the center by an angle of , followed by inversion through the center of the diagram, to reach the position P 3 below the plane, indicated by the small circle
rotation around the center by an angle of , followed by inversion through the center of the diagram, to reach the position P 3 below the plane, indicated by the small circle