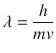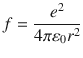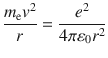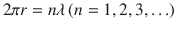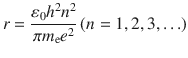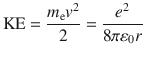1.1 Matter and Atom
By the difference of scale, matter is largely classified into the three: solid, molecule and cluster (nano-cluster), as shown in Fig.. Molecule and cluster exist in the basic three fundamental states: gas, liquid and solid (molecular solid). In quantum chemistry, electronic structure is normally discussed in three fundamental states. As the extreme environment, matter exists as plasma and superconducting states. In plasma state, matter is divided into positively charged ion and negatively charged electron at very high temperature. It has been considered that most of matter in space exists as plasma state. On the other hand, in superconducting state, electric resistance becomes zero at very low temperature, though matter keeps the same crystal structure.
Fig. 1.1
Basic three fundamental states of matter
The basis unit of matter is atom. Atom consists of quantum particles such as electron, proton and neutron. As they belong to Fermi particle, the spin angular momentum becomes half-integer. Atom has an atomic nucleus at the centre, consisting of proton and neutron. As is well known, there are several kinds of atoms in space. The kind of atom is called element. Element is represented by atomic number ( Z ) that corresponds to the total number of protons. For example, the elements of Z = 1, 2 and 3 denote hydrogen, helium and lithium, respectively. When the same element has the different total number of neutrons, it is called isotope. As the magnitude of charge density of proton is e , the total charge density of atomic nucleus becomes + Ze . Z electrons are allocated around atomic nucleus. Note that the magnitude of electron charge density is e .
1.2 Wave-Particle Duality
Quantum particle is defined as particle with wave-particle duality. The wave property is incorporated through the concept of matter wave.
where is the wave-length of matter wave: h is Plank constant; m is the mass of quantum particle; v is the velocity of quantum particle. In electron, m denotes the mass of electron, which is expressed as m e. Though the energy of classical particle continuously changes, quantum particle has the discrete energy.
1.3 Bohr Model
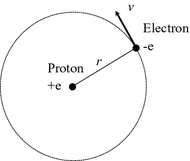
Niels Bohr proposed a theoretical hydrogen model, which is well known as Bohr model, to express positions of electron and atomic nucleus, under consideration of wave-particle durability. In Bohr model, proton is located at atomic centre, and electron rotates around atomic centre, as shown in Fig.. The driving factor of the rotation is the Coulomb interaction ( f ) between proton and electron:
where 0 is dielectric constant of vacuum; r is orbit radius. The centrifugal force, which is obtained from the classical equation of circular motion, is equal to the Coulomb interaction.
Fig. 1.2
Schematic drawing of Bohr model. Proton is located at atomic centre, and electron goes around an orbit
The equation implies that quantum effect is taken into account, by applying the concept of matter wave to electron. Electron goes around an orbit, and orbit distance is mathematically determined to be 2 r . It must be also integer-multiple of wave-length of matter wave.
By the substitution of Eq. (), it is rewritten:
By the substitution of Eq. (), the orbit radius of hydrogen is obtained:
As orbit radius depends on integer ( n ), it is found that orbit radius is quantized. It implies that orbital radius has only discrete value. The orbit radius of n = 1 is called Bohr radius. The value is estimated to be 0.5292 .
Let us consider an electron energy. It is obtained by the summation of electron kinetic energy (KE) and potential energy (PE). In classical manner, KE is given by
From Coulombs law, PE is given by
It is defined that PE is zero, when electron is infinitely apart from proton. Hence, potential energy exhibits negative value. Finally, the total energy of electron is given by