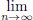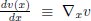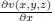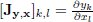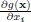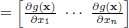Contents
Landmarks
Page Navigation
Probabilistic Machine Learning for Civil Engineers
2020 Massachusetts Institute of Technology
This work is subject to a Creative Commons CC-BY-NC-ND license.

Subject to such license, all rights are reserved.
This book was set in  by the author.
by the author.
Library of Congress Cataloging-in-Publication Data
Names: Goulet, James-A., author.
Title: Probabilistic machine learning for civil engineers / James-A. Goulet.
Description: Cambridge, Massachusetts : The MIT Press, 2020. | Includes bibliographical references and index.
Identifiers: LCCN 2019027152 | ISBN 9780262358019
Subjects: LCSH: Machine learning. | Probabilities.
Classification: LCC Q325.5 .G68 2020 | DDC 006.3/1dc23
LC record available at https://lccn.loc.gov/2019027152
d_r0
Acknowledgments
I would like to acknowledge the help I have received from colleagues, students, and friends in the process of writing this book. I especially thank Jonathan Jalbert, Shervin Khazaeli, Saeid Amiri, Sbastien Le Digabel, Marco Broccardo, Luong-Ha Nguyen, Rocio Lilen Segura, and Gerd Brandstetter for helping me with reviewing the manuscript. I also acknowledge the feedback I have received from many students who attended my CIV6540 graduate class at Polytechnique Montreal. I want to thank Michel Goulet, who contributed to the book with several of his photos; as well as Daphne and Daniel Dethier, who provided helpful insights during the design of the book cover. I thank the anonymous reviewers who took the time to read the manuscript and whose comments were integrated into the final version.
In a broader perspective, I would like to thank my family for their inexhaustible support over the years. Also, I want to recognize the constructive influence from my advisers, who guided me since the beginning of my university years: Andr Picard, Mario Fafard, Ian F.C. Smith, and last but certainly not least, Armen Der Kiureghian, who was an inspiration through his lectures and mentoring.
Finally, I want to acknowledge the exceptional freedom I was allowed to have as a young professor by my host institution, Polytechnique Montreal. Without it, I do not see how this book would have been possible.
General Mathematical Symbols
Real domain (, ) |
+ | Real positive domain (0, ) |
Real integer domain { , 1, 0, 1, 2, } |
(0, 1) | Continuous close interval between 0 and 1, which includes 0 and 1 |
(0, 1] | Continuous open interval between 0 and 1, which includes 0 and not 1 |
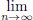
| A limit when n tends to infinity |
For all |
: | Such that |

| The true value for x |

| An approximation of x |
Sum operation |
The negation symbol |
Product operation |
dx | Integral operation with respect to x |
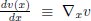
| Derivative or gradient of v(x) with respect to x |
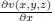
| Partial derivative of v(x, y, z) with respect to x |
|x| | Absolute values of x |
Approximately equal |
Proportional to |
Equivalent |
ln(x) loge(x) | Natural logarithm of x ln(exp(x)) = x |
exp(x) ex | Exponential function of x, = 2.71828x, exp(ln(x)) = x |
x | An infinitesimal interval for x |
AB | A implies B and B implies A |
Linear Algebra
x | A scalar variable |
x | A column vector, x = [x1x2x X ] T |
X | A matrix |
xi [x]i | ith element of a vector |
xij [X]ij | {i, j}th element of a matrix |
X = diag(x) | Square matrix X where the terms on the main diagonal are the elements of x and 0 elsewhere |
x = diag(X) | Vector x consisting in the main diagonal terms of a matrix X |
I | The identity matrix, i.e., a square matrix with 1 on the main diagonal and 0 elsewhere |
blkdiag(A, B) | Block diagonal matrix where matrices A and B are concatenated on the main diagonal of a single matrix |
T | Transposition operator : [X]ij = [XT ]ji |
Scalar product |
Matrix multiplication |
Hadamar (element-wise) product |
||x||p | Lp-norm of a vector x |
det(A) |A| | Determinant of a Matrix A |
tr(A) | Sum of the elements on the main diagonal of A |
A transformation from a space to another |
Jy,x | The Jacobian matrix so that 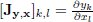 |
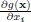
| Partial derivative of g(x) with respect to the ith variable xi |
g(x) | A gradient vector, 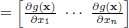 |
Next page










 by the author.
by the author.