Edcorner Learning - 77 Python Advanced Programming Exercises

Python is a general-purpose interpreted, interactive, object- oriented, and a powerful programming language with dynamic semantics. It is an easy language to learn and become expert. Python is one among those rare languages that would claim to be both easy and powerful. Python's elegant syntax and dynamic typing alongside its interpreted nature makes it an ideal language for scripting and robust application development in many areas on giant platforms. Python helps with the modules and packages, which inspires program modularity and code reuse. The Python interpreter and thus the extensive standard library are all available in source or binary form for free of charge for all critical platforms and can be freely distributed.

Learning Python doesn't require any pre- requisites. However, one should have the elemental understanding of programming languages. This Book consist of 77 python advanced exercise High level of coding exercises to practice different topics. In each exercise we have given the exercise coding statement you need to complete and verify your answers. We also attached our own input output screen of each exercise and their solutions. Learners can use their own python compiler in their system or can use any online compilers available.

We have covered all level of exercises in this book to give all the learners a good and efficient Learning method to do hands on python different scenarios.

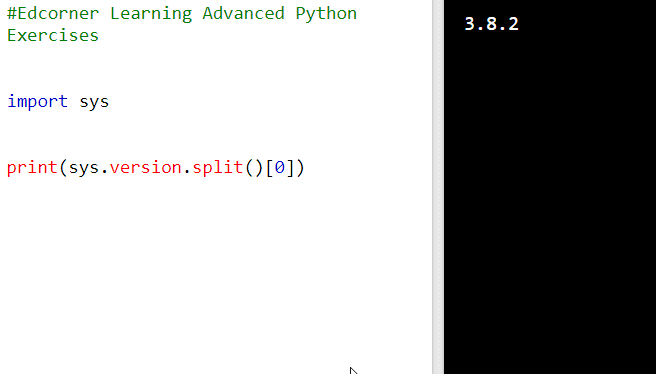
Print the Python version to the console. Expected result: 3.8.2 2. All natural numbers divisible by 5 or 7 less than 20 are: [0, 5, 7, 10, 14, 15]. The sum of these numbers is: 51. In this exercise, we treat zero as a natural number.

Find the sum of all numbers that are divisible by 5 or 7 less than 100. Present the solution in the form of a function called calculate(). In response, call calculate() function and print the result to the console. Expected result: 1580 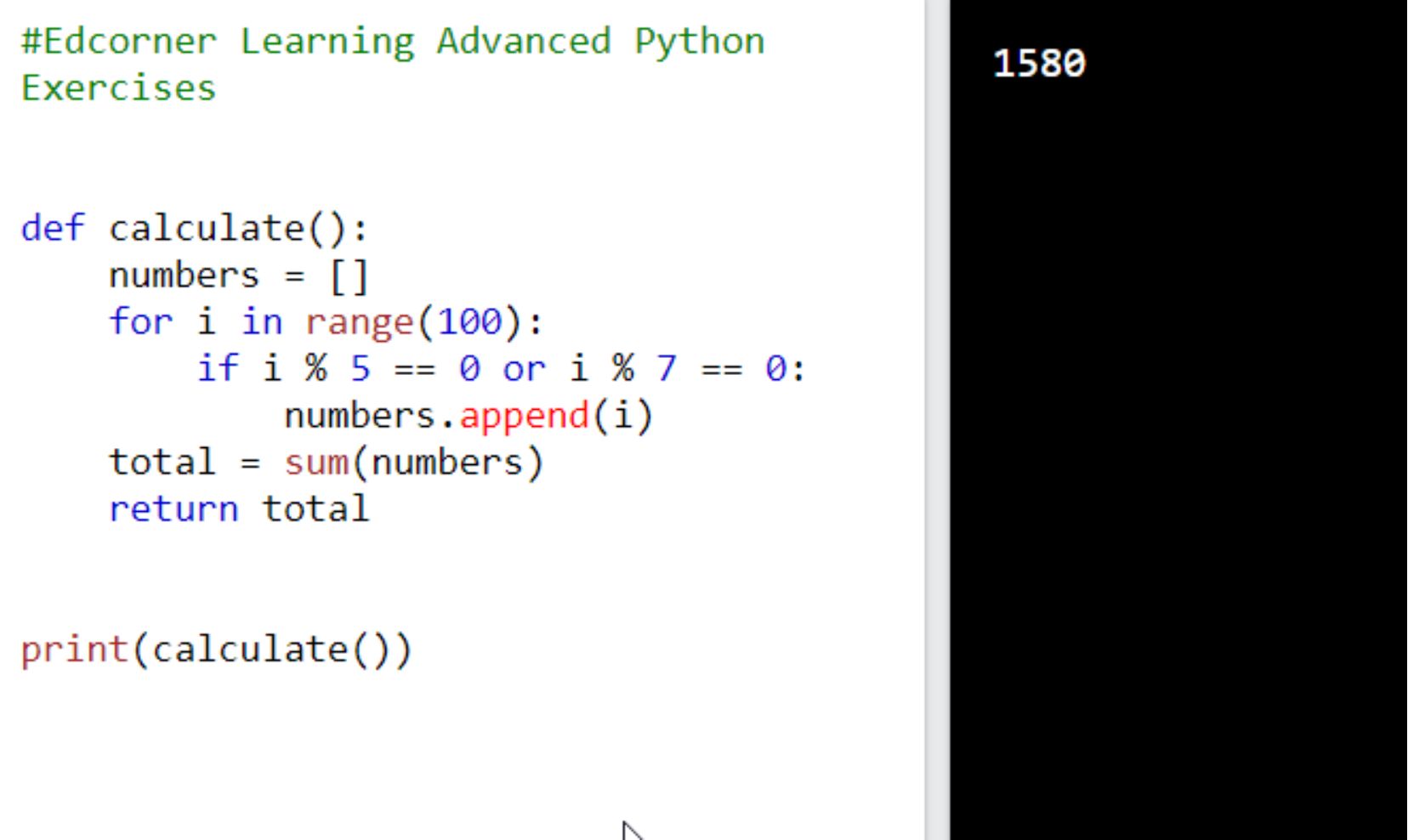Another Solution: 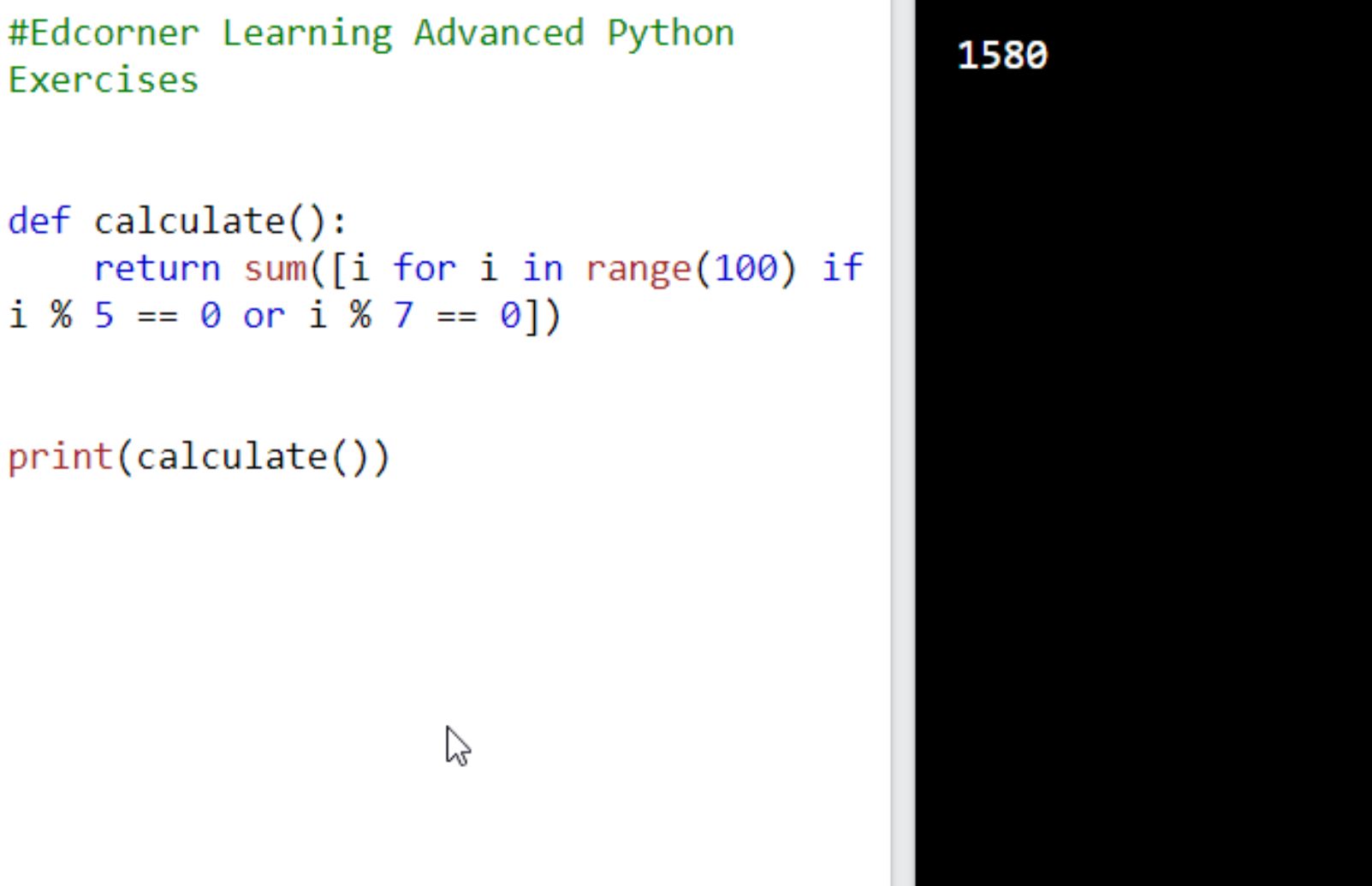3. Consider the Fibonacci sequence. It is a sequence of natural numbers defined recursively as follows: the first element of the sequence is 0 the second element of the sequence is 1 each next element of the sequence is the sum of the previous two elements The beginning of the Fibonacci sequence: Find the sum of all even elements of the Fibonacci sequence with values less than 1,000,000 (1 million).

Present the solution in the form of a function called calculate( ) . In response, call calculate( ) function and print the result to the console. Expected result: 1089154 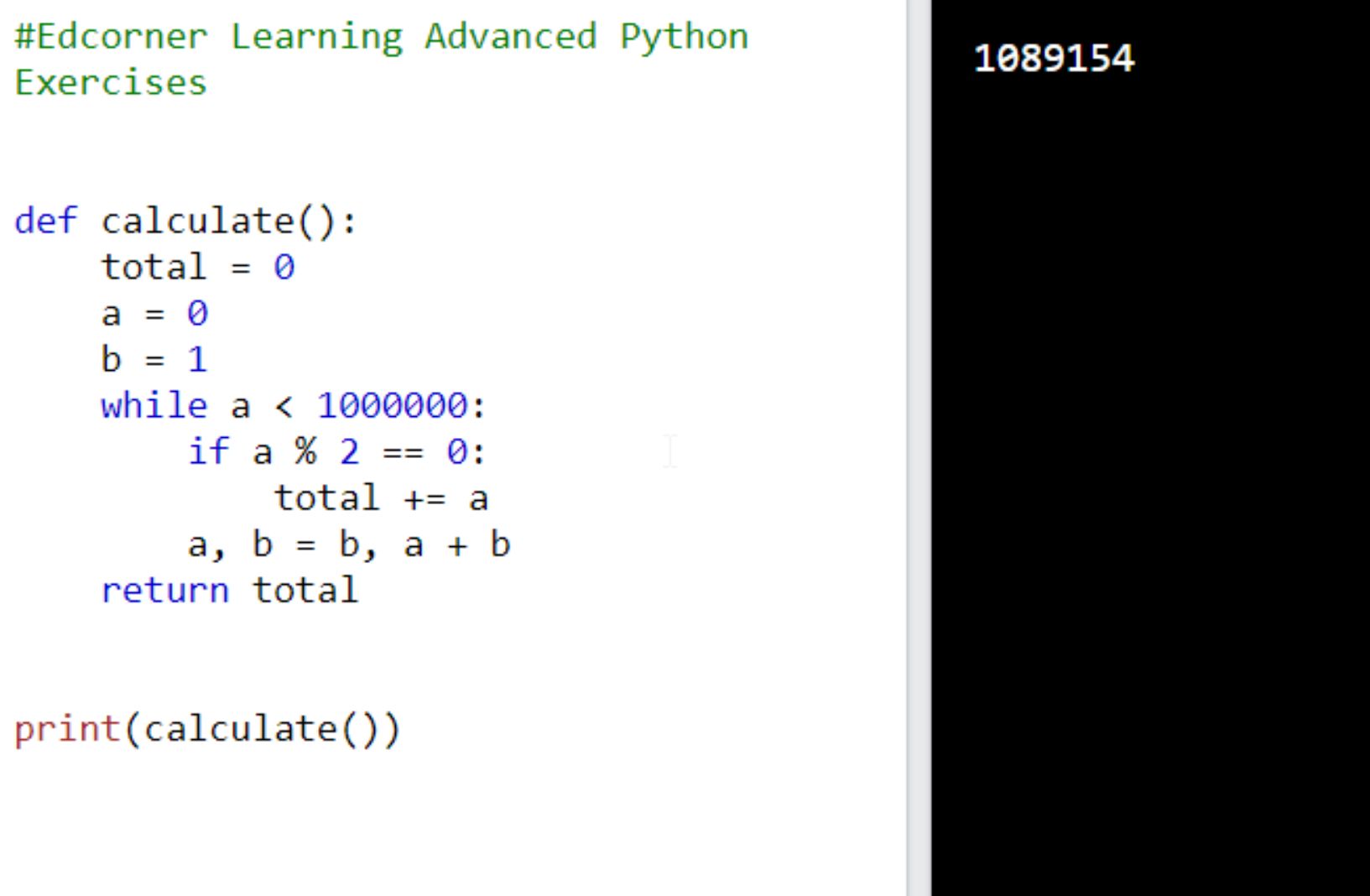4. In number theory, integer factorization is the decomposition of a composite number into a product of smaller integers. If these factors are further restricted to prime numbers, the process is called prime factorization. Examples of prime numbers: 2, 3, 5, 7, 11, 13, 17, 19, ...

Reminder: The number 1 is not a prime number. A number that is greater than 1 and is not a prime is called a composite number. Examples of composite numbers: 4, 6, 8, 9, 10, 12, 14, 15, 16, ... We can break down a composite number into prime factors. For example: 15=3*5 36=2*2*3*3 48=2*2*2*2*3 Implement a function that takes a natural number as an argument and returns a list containing the prime factorization of that number. Present the solution in the form of a function called Calculate() .

Example: [IN]: calculate(48) [OUT]: [2, 2, 2, 2, 3] You just need to implement the function. The tests run several test cases to validate the solution. Solution : def calculate(number): i = 2 factors = [] while i * i <= number: if not number % i == 0: i += 1 else: number = number // i factors.append(i) if number > 1: factors.append(number) return factors 5. In number theory, integer factorization is the decomposition of a composite number into a product of smaller integers. If these factors are further restricted to prime numbers, the process is called prime factorization. Examples of prime numbers: 2, 3, 5, 7, 11, 13, 17, 19, ...

Reminder: The number 1 is not a prime number. A number that is greater than 1 and is not a prime is called a composite number. Examples of composite numbers: 4, 6, 8, 9, 10, 12, 14, 15, 16, ... We can break down a composite number into prime factors. For example: 15 = 3*5 36=2*2*3*3 The largest prime factor for 15 is 5, and for 36 is 3. Using the previous exercise, implement a function that takes a natural number as an argument and returns the greatest prime factor of that number.

Present the solution in the form of a function called calculate() . Example: [IN]: calculate(13195) [OUT]: 29 Solution: def calculate(number): i = 2 factors = [] while i * i <= number: if not number % i == 0: i += 1 else: number = number // i factors.append(i) if number > 1: factors.append(number) return max(factors) 6. Consider the palindromic numbers. A palindromic or symmetric number is a number that does not change when you write its digits in reverse order. Some examples of palindromic numbers: 2882 29492 Implement a function that returns the number of all three-digit palindromic numbers. Present the solution in the form of a function called calculate( ) .

In response, call calculate( ) function and print the result to the console. Expected result: 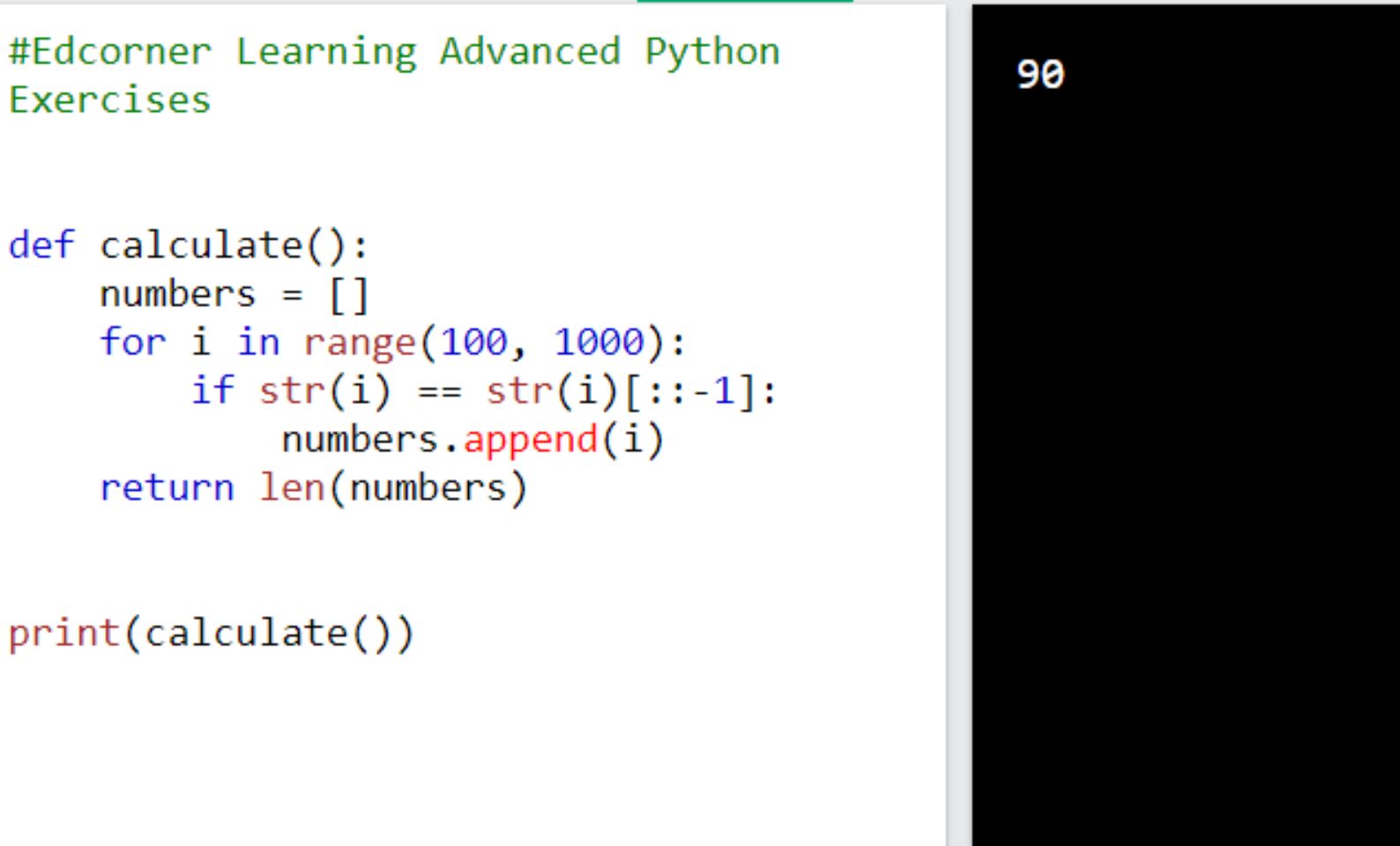7. Consider the palindromic numbers. A palindromic or symmetric number is a number that does not change when you write its digits in reverse order. Some examples of palindromic numbers: 2882 29492 Implement a function that returns the largest palindromic number resulting from the product of two-digit numbers. Present the solution in the form of a function called calculate( ) .

In response, call calculate( ) function and print the result to the console. Expected result: 9009 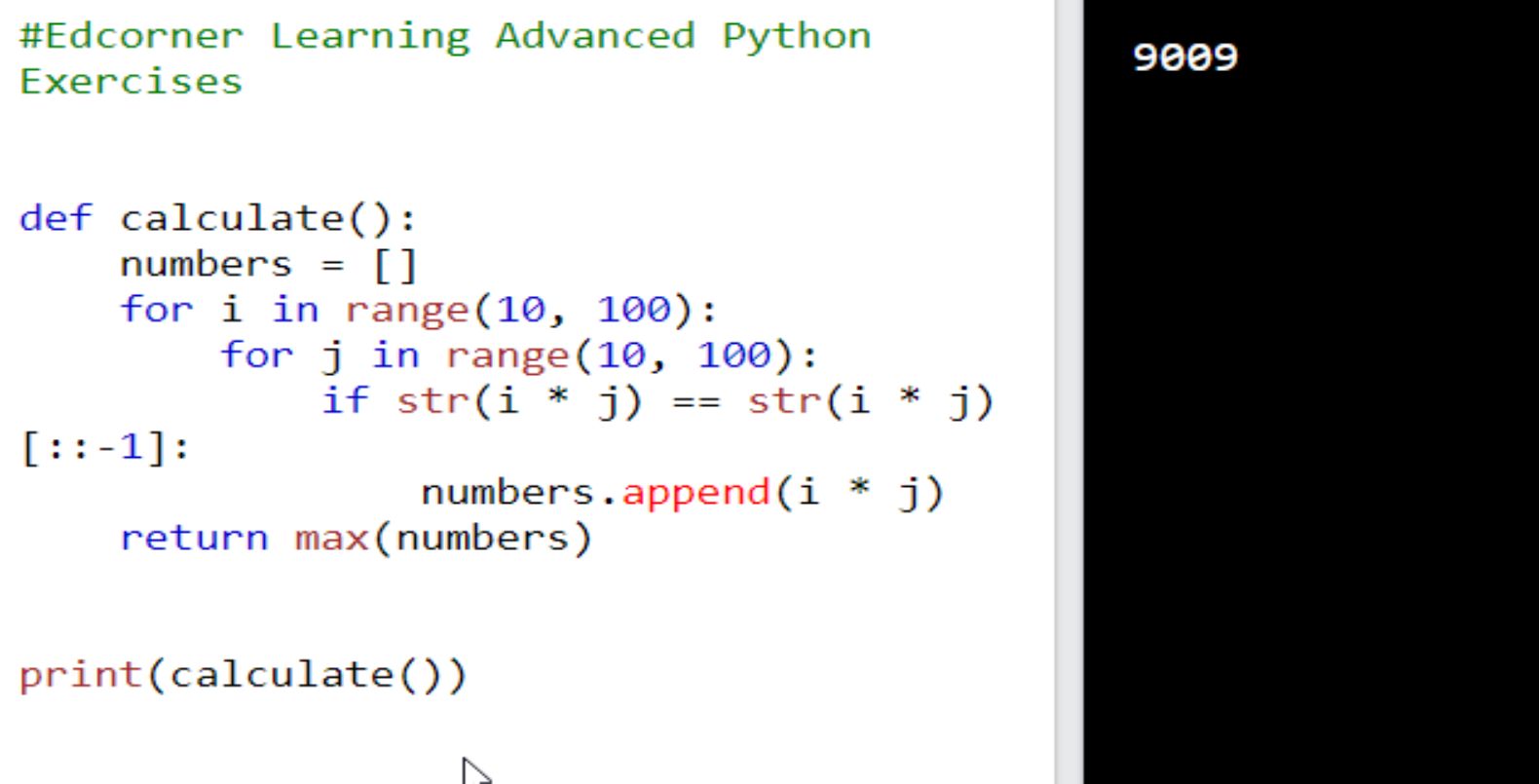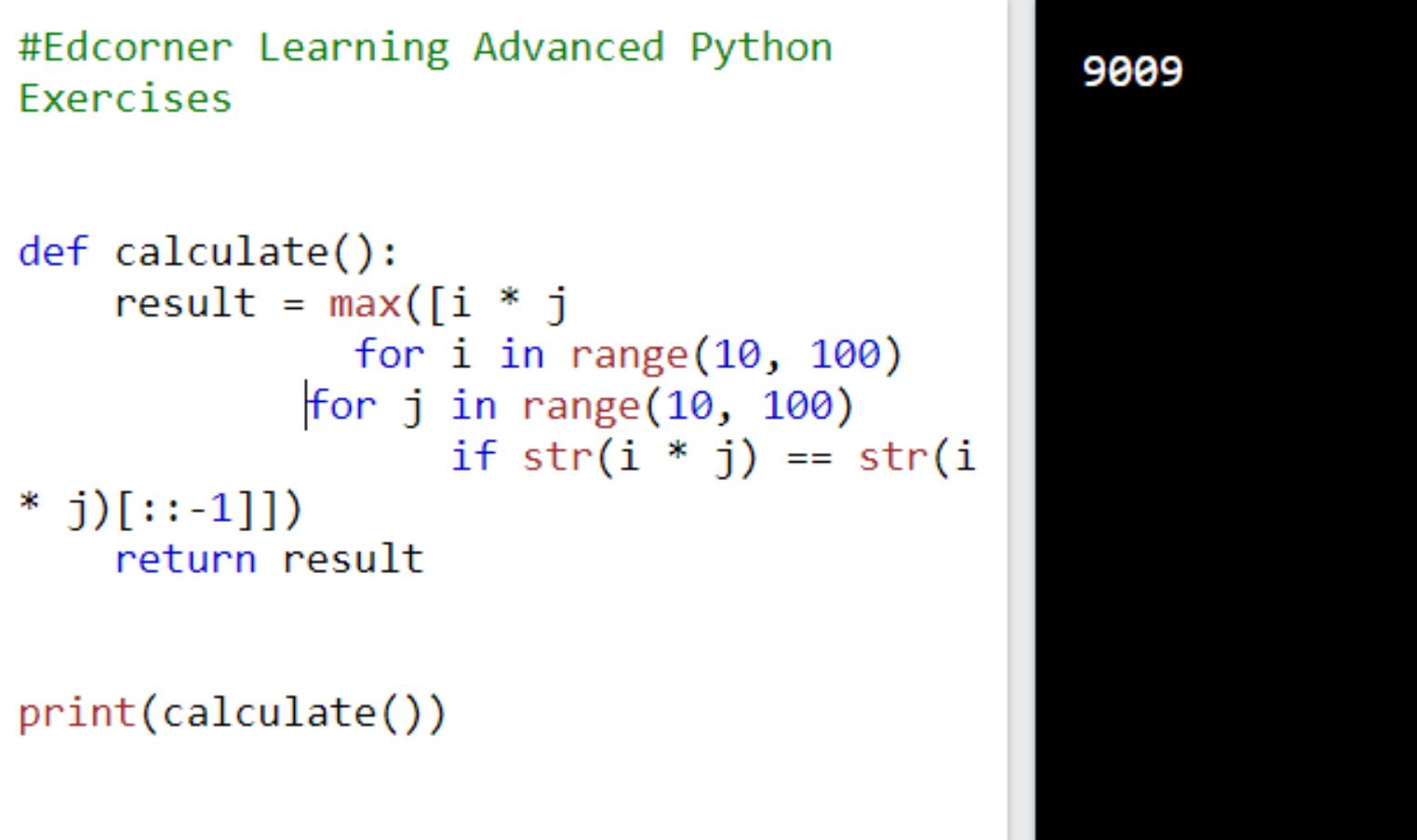Another Solution: Greatest Common Divisor (GCD) of two integers - this is the largest natural number that divides both of these numbers without a remainder. For example, for numbers 32 and 48, the greatest common divisor is 16, which we can write GCD(32, 48) = 16 . Implement a function called greatest_common_divisor() that determines the greatest common divisor of two numbers. Implement a function called greatest_common_divisor() that determines the greatest common divisor of two numbers. Example: [IN]: greatest_coFimon_divisor(32, 48) [OUT]: 16 You just need to implement the function.

The tests run several test cases to validate the solution. Solution: def greatest_common_divisor(a, b): while b: a, b = b, a % b return a 9. A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. Examples of prime numbers: 2, 3, 5, 7, l1, 13, 17, 19, ... Implement a function called is_prime( ) that takes a natural number as an argument and checks if it is a prime number. In the case of a prime number, the function returns True, otherwise False.