K. S. Thyagarajan - Introduction to Digital Signal Processing Using MATLAB with Application to Digital Communications

Introduction to Digital Signal Processing Using MATLAB with Application to Digital Communications — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Introduction to Digital Signal Processing Using MATLAB with Application to Digital Communications" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...112

Springer International Publishing AG, part of Springer Nature 2019

K.S. Thyagarajan Introduction to Digital Signal Processing Using MATLAB with Application to Digital Communications

1. Introduction

K. S. Thyagarajan 1

(1)

Extension Program, University of California, San Diego, San Diego, CA, USA

K. S. Thyagarajan

Electronic supplementary material:

The online version of this article ( https://doi.org/10.1007/978-3-319-76029-2_1 ) contains supplementary material, which is available to authorized users.

The field of digital signal processing is well matured and has found applications in most commercial as well as household items. It started in the 1960s when computers were used only in the academic institutions. Moreover, these computers were built around vacuum tubes with limited memory and slow processing power. This situation was not conducive to rapid advancements in digital signal processing theory. As the computer technology advanced due to the invention of microprocessors and semiconductor memories, the field of digital signal processing also simultaneously progressed. Today, digital signal processing is used in a myriad of fields such as communications, medicine, forensic, imaging, and music to name a few. It is, therefore, necessary for an aspirant to learn the basics of digital signal processing so as to be able to apply his or her knowledge in this field to career advancement.

1.1 What Is Digital Signal Processing

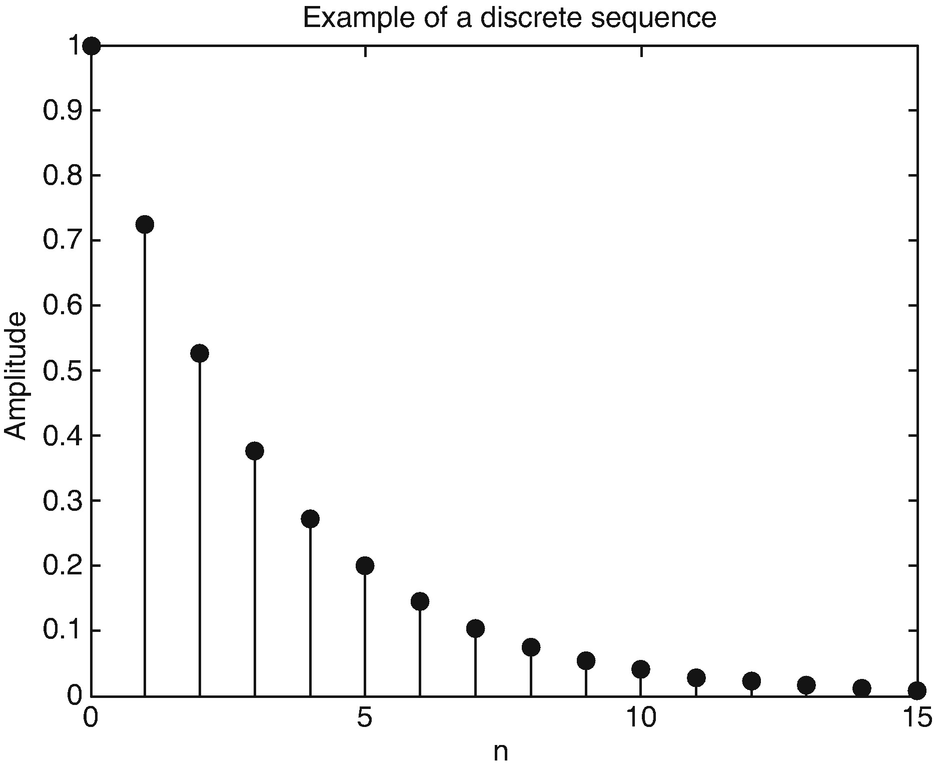
A signal can be considered, for example, as a voltage or current that varies as a function of time. A digital signal, on the other hand, can be any sequence of numbers that can be stored in a computer memory or a piece of hardware. Or, it may be acquired in real time from a signal source. If this sequence of numbers is related or meaningful, then, it is a useful signal or just signal. Figure b shows this exactly.

Fig. 1.1

An example of a signal sequence

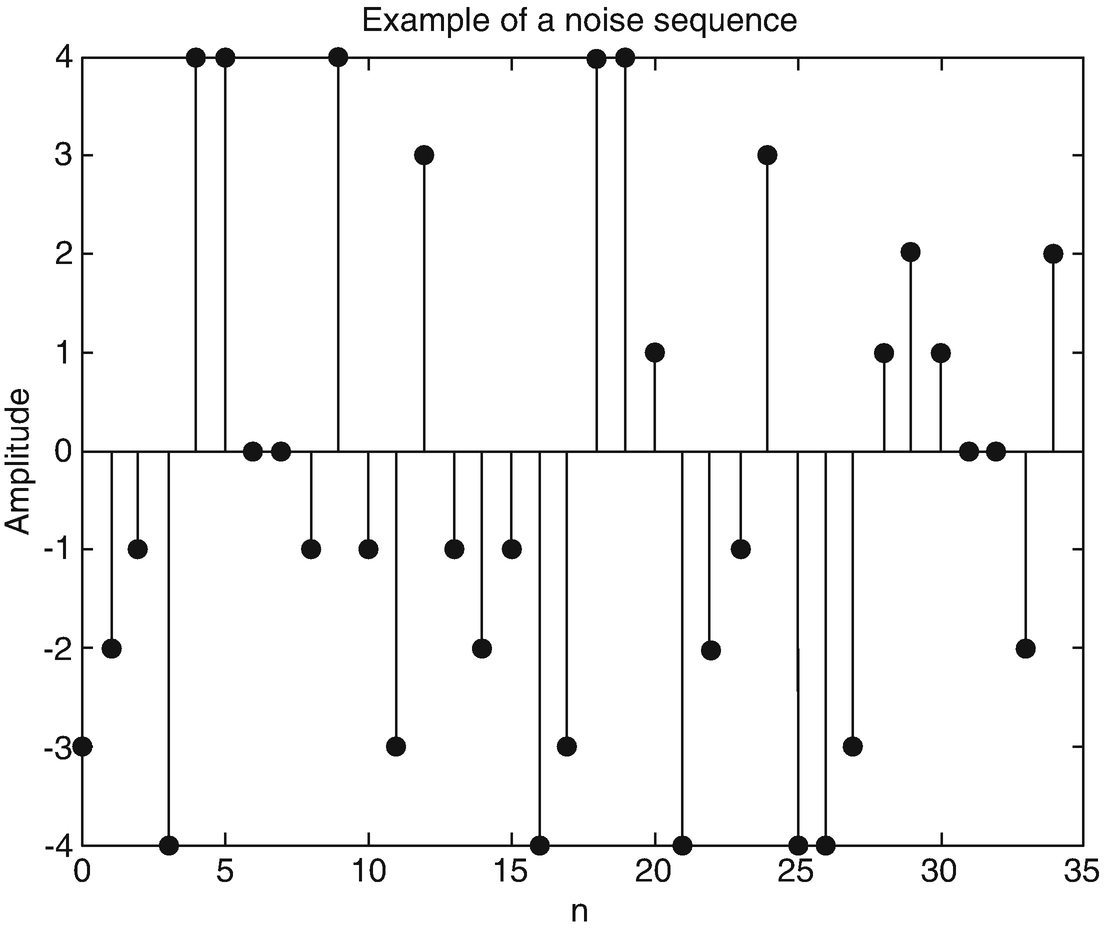
Fig. 1.2

An example of a random or noise sequence

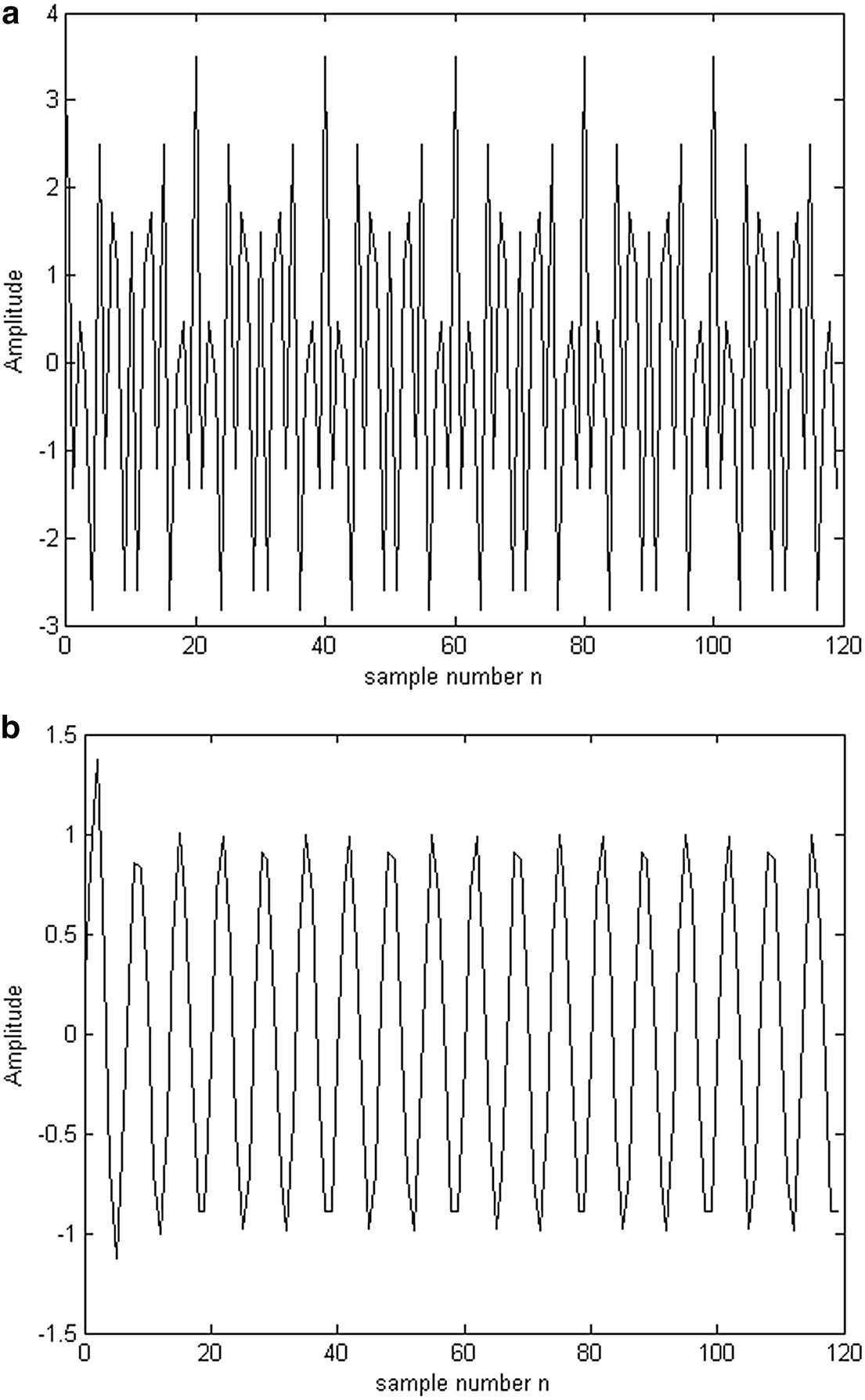
Fig. 1.3

Filtering as an example of digital signal processing. ( a ) Input signal consisting of 1500 and 4000 Hz sinusoidal components. ( b ) Filtered signal consisting of only the 1500 Hz sinusoid

In digital image processing, for example, one can increase or decrease the sharpness by a suitable filtering operation. Figure b.

Fig. 1.4

An example of digital image sharpening using an appropriate filtering operation . ( a ) Original image lacking in sharpness, ( b ) sharpened image

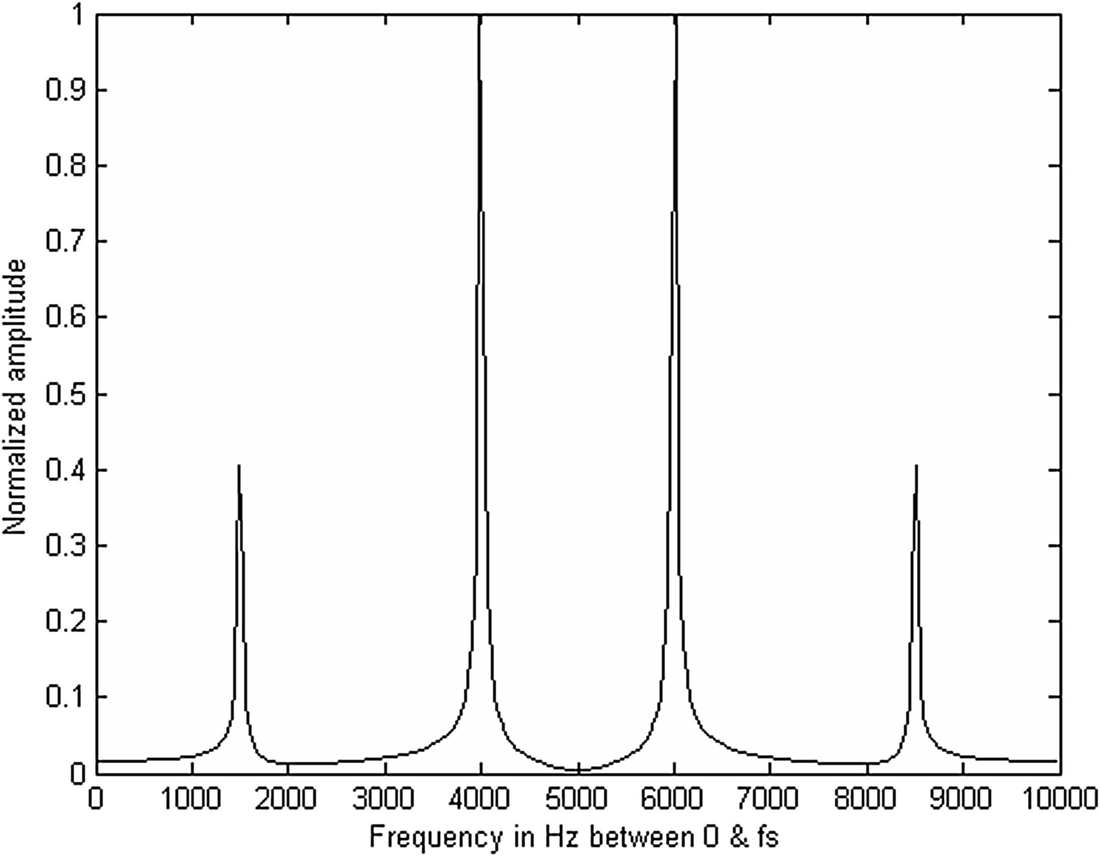
Another digital signal processing operation may be to estimate the frequency spectrum of a signal. This is useful in speech compression . An example of frequency spectrum is shown in Fig.. As can be seen, there are two frequencies present in the signal, one at 1500 Hz and the other at 4000 Hz. Note that the spectrum is symmetric about 5000 Hz, which is half the sampling frequency. We will discuss the sampling process in detail later in the book. The amplitude of the 1500 Hz component relative to that of the 4000 Hz component is 0.4 as shown in the figure. As mentioned, there are numerous operations to choose from in processing a digital signal. It all depends on a particular application at hand.

Fig. 1.5

Frequency spectrum of the signal in Fig. a. There are two frequencies present, one at 1500 Hz and the other at 4000 Hz

1.2 A Few Applications of Digital Signal Processing

As mentioned above, there are numerous areas where digital signal processing is used. We will describe here a few applications of digital signal processing that will motivate the readers to go deeper into it.

1.2.1 Audio/Speech Processing

One of the most widely used aspects of speech in communications is speech compression. As landline and wireless telephony are ubiquitous, voice bandwidth is constrained to a minimum of 4 kHz to conserve bandwidth or, equivalently, to accommodate more subscribers. A voice with this bandwidth is quite intelligible and discernible. One of the voice compression methods uses what is known as linear prediction . Since there is a high correlation from sample to sample in speech signals, it is more efficient to store or transmit the difference between a sample and its predicted value rather than storing or transmitting the actual sample values. The predicted value of a current sample is obtained as a linear combination of the previously predicted samples. This, therefore, forms a feedback loop and can be considered a digital filtering operation.

In another form of speech compression, a bank of filters is used to separate the speech signal into different frequency bands or subbands and then coding each subband with a different number of bits of quantization based on the importance of each subband. This is known as sub-band coding . Of course, sub-band coding uses digital signal processing. One form of an efficient speech compression system extracts features of a speech signal first and then encodes the extracted features for storage or transmission. This process uses digital signal processing. At the receiving side, these features are used to synthesize speech, which again uses heavily digital signal processing. In music too various digital signal processing methods are used to produce sound effects. These are just a few cases where digital signal processing is involved in audio/speech signals.

1.2.2 Digital Communications

In digital communications , a signal such as voice or music to be transmitted is first converted to PCM (pulse code modulation) signals, which can then be transmitted as such or can be used to modulate a carrier signal. If no carrier modulation is used, the binary signal transmission is called baseband transmission. In baseband transmission, a sequence of binary data consisting of zeros and ones is transmitted as a sequence of two waveforms. The binary 0 corresponds to the waveform s 0( t ), 0 t T b , and the binary 1 corresponds to the waveform s 1( t ), 0 t T b , where T b is the duration of each bit of data. During the transmission of the baseband signals through a channel, the data is corrupted by electrical noise. An optimal baseband receiver correlates the received signal with a replica of each waveform and decides which binary symbol was transmitted, by comparing the outputs of the two correlators. Instead of the correlator, one can also use what is known as matched filter to recover the transmitted binary data. Both correlators and matched filters can be realized as digital filtering operations.

Though the abovementioned receiver operation seems perfect, there is a problem due to finite bandwidth of the transmission channel. As a result, the sequence of transmitted binary waveforms can interfere with neighboring waveforms. This interference is called the inter-symbol interference (ISI) . One way of minimizing the ISI is to design proper waveforms corresponding to the binary zero and one. These waveforms can be sampled versions and stored in memory. Another ISI mitigation method is to use linear equalizers , where the nonlinear group delay of the channel is equalized or linearized using digital FIR filters. Similar digital signal processing operations are used extensively in spread spectrum communications systems.

Next page

1234567...112

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Introduction to Digital Signal Processing Using MATLAB with Application to Digital Communications»

Look at similar books to Introduction to Digital Signal Processing Using MATLAB with Application to Digital Communications. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

João Marques de Carvalho

Digital Signal Processing

Orhan Gazi

Principles of Signals and Systems

Narayan Panigrahi

Brain Computer Interface: EEG Signal Processing

Dipali Bansal

Real-Time Data Acquisition in Human Physiology: Real-Time Acquisition, Processing, and Interpretation—A MATLAB-Based Approach

Sozański

Digital Signal Processing in Power Electronics Control Circuits

Samir I. Abood

Digital Signal Processing: A Primer with MATLAB®

Orhan Gazi

Understanding Digital Signal Processing

Eric Tarr

Hack Audio: An Introduction to Computer Programming and Digital Signal Processing in MATLAB

Magda Y.

BeagleBone Black Interfacing: hardware and software

Allen B. Downey

Think DSP: Digital Signal Processing in Python

Richard G. Lyons

The Essential Guide to Digital Signal Processing

Richard Baraniuk

Signals and Systems

Discussion, reviews of the book Introduction to Digital Signal Processing Using MATLAB with Application to Digital Communications and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.