Dirk Taeger - Statistical Hypothesis Testing with SAS and R

This edition first published 2014

2014 John Wiley & Sons, Ltd

Registered office

John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex, PO19 8SQ, United Kingdom

For details of our global editorial offices, for customer services and for information about how to apply for permission to reuse the copyright material in this book please see our website at www.wiley.com.

The right of the author to be identified as the author of this work has been asserted in accordance with the Copyright, Designs and Patents Act 1988.

All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, except as permitted by the UK Copyright, Designs and Patents Act 1988, without the prior permission of the publisher.

Wiley also publishes its books in a variety of electronic formats. Some content that appears in print may not be available in electronic books.

Designations used by companies to distinguish their products are often claimed as trademarks. All brand names and product names used in this book are trade names, service marks, trademarks or registered trademarks of their respective owners. The publisher is not associated with any product or vendor mentioned in this book.

Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best efforts in preparing this book, they make no representations or warranties with respect to the accuracy or completeness of the contents of this book and specifically disclaim any implied warranties of merchantability or fitness for a particular purpose. It is sold on the understanding that the publisher is not engaged in rendering professional services and neither the publisher nor the author shall be liable for damages arising herefrom. If professional advice or other expert assistance is required, the services of a competent professional should be sought.

Library of Congress Cataloging-in-Publication Data

Taeger, Dirk, author.

Statistical hypothesis testing with SAS and R / Dirk Taeger, Sonja Kuhnt.

pages cm

Includes bibliographical references and index.

ISBN 978-1-119-95021-9 (hardback)

1. Statistical hypothesis testing. 2. SAS (Computer program language) 3. R (Computer program language) I. Kuhnt, Sonja, author. II. Title.

QA277.T34 2014

519.502855133 dc23

2013041089

A catalogue record for this book is available from the British Library.

ISBN: 978-1-119-95021-9

To Thomas and Katharina

Preface

Statistical hypothesis testing has been introduced almost one hundred years ago and has become a key tool in statistical inferences. The number of available tests has grown rapidly over the decades. With this book we present an overview of common statistical tests and how to apply them in SAS and R. For each test a general description is provided as well as necessary prerequisites, assumptions and the formal test problem. The test statistic is stated together with annotations on its distribution. Additionally two examples, one in SAS and one in R, are given. Each example contains the code to perform the test using a tiny dataset, along with output and remarks that explain necessary program parameters.

This book is addressed to you, whether you are an undergraduate student who must do course work, a postgraduate student who works on a thesis, an academic or simply a practitioner. We hope that the clear structure of our presentation of tests will enable you to perform statistical tests much faster and more directly, instead of searching through documentation or looking on the World Wide Web. Hence, the book may serve as a reference work for the beginner as well as someone with more advanced knowledge or even a specialist.

The book is organized as follows. In the first part we give a short introduction to the theory of statistical hypothesis testing and describe the programming philosophy of SAS and R. This part also contains an example of how to perform statistical tests in both programming languages and of the way tests are presented throughout the book. The second part deals with tests on normally distributed data and includes well-known tests on the mean and the variance for one and two sample problems. Part three explains tests on proportions as parameters of binomial distributions while the fourth part deals with tests on parameters of Poisson and exponential distributions. The fifth part shows how to conduct tests related to the Pearson's, Spearman's and partial correlation coefficients. With Part six we change to nonparametric tests, which include tests on location and scale differences. Goodness-of-fit tests are handled in Part seven and include tests on normality and tests on other distributions. Part eight deals with tests to assess randomness. Fisher's exact test and further tests on contingency tables are covered in Part nine, followed by tests on outliers in Part ten. The book finished with tests in regression analysis. We provide the used datasets in the appendices together with some tables on critical values of the most common test distributions and a glossary.

Due to the numerous statistical tests available we naturally can only present a selection of them. We hope that our choice meets your needs. However, if you miss some particular tests please send us an e-mail at: book@d-taeger.de . We will try to publish these missing tests on our book homepage. No book is free of errors and typos. We hope that the errors follow a Poisson distribution, that is, the error rate is low. In the event that you find an error please send us an e-mail. We will publish corrections on the accompanying website ( http:\\www.d-taeger.de ).

Last but not least we would like to thank Wiley for publishing our book and especially Richard Davies from Wiley for his support and patience. We hope you will not reject the null hypothesis that this book is useful for you.

Dirk Taeger
Sonja Kuhnt
Dortmund

The theory of statistical hypothesis testing was basically founded one hundred years ago by the Britons Ronald Aylmer Fisher, Egon Sharpe Pearson, and the Pole Jerzy Neyman. Nowadays it seems that we have a unique test theory for testing statistical hypothesis, but the opposite is true. On one hand Fisher developed the theory of significance testing and on the other hand Neyman and Pearson the theory of hypothesis testing.

Whereas with the Fisher theory the formulation of a null hypothesis is enough, Neyman's and Pearson's theory demands alternative hypotheses as well. They open the door to calculating error probabilities of two kinds, namely of a false rejection (type I error) and of a false acceptance (type II error) of the null hypothesis. This leads to the well known NeymanPearson lemma which helps us to find the best critical region for a hypothesis test with a simple alternative. The largest difference of both schools, however, are the Fisherian measure of evidence (p-value) and the NeymanPearson error rate ().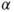

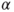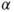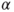With the NeymanPearson theory the error rate is fixed and must be defined before performing the test. Within the Fisherian context the p-value is calculated from the value of the test statistic as a quantile of the test statistic distribution and serves as a measure of disproving the null hypothesis. Over the decades both theories have merged together. Today it is common practice and described by most textbooks to perform a NeymanPearson test and, instead of comparing the value of the test statistic with the critical region, to decide from the p-value. As this book is on testing statistical hypothesis with SAS and R we follow the common approach of mixing both theories. In SAS and R the critical regions are not reported, only p-values are given. We want to make the reader aware of this situation. In the next two chapters we shortly summarize the concept of statistical hypothesis testing and introduce the performance of statistical tests with SAS and R.