Scott Hartshorn - Hypothesis Testing: A Visual Introduction to Statistical Significance

If you are looking for a short beginners guide packed with visual examples, this booklet is for you.

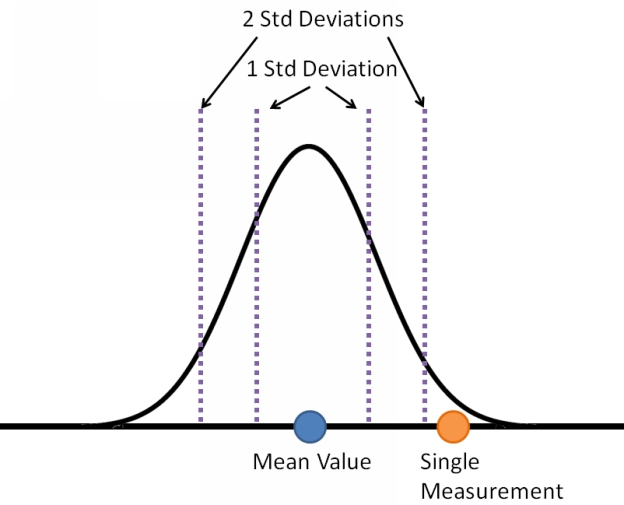
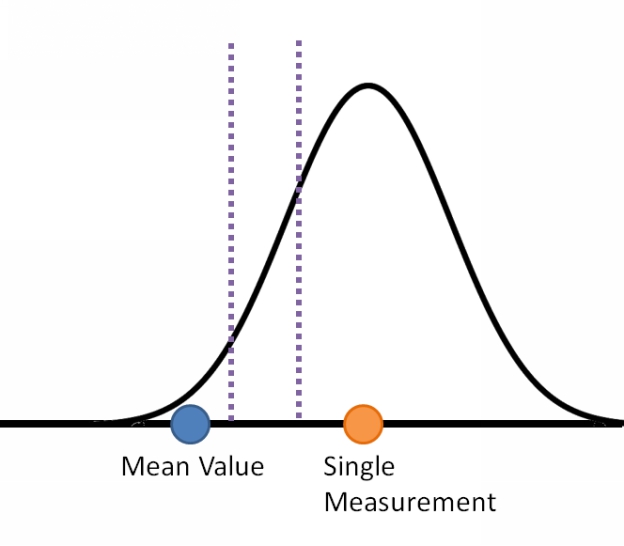
Statistical significance is a way of determining if an outcome occurred by random chance, or did something cause that outcome to be different than the expected baseline. Statistical significance calculations find their way into scientific and engineering tests of all kinds, from medical tests with control group and a testing group, to the analysis of how strong a newly made batch of parts is. Those same calculations are also used in investment decisions.

This book goes through all the major types of statistical significance calculations, and works through an example using them, and explains when you would use that specific type instead of one of the others. Just as importantly, this book is loaded with visual examples of what exactly statistical significance is, and the book doesnt assume that you have prior in depth knowledge of statistics or that use regularly use an advanced statistics software package. If you know what an average is and can use Excel, this book will build the rest of the knowledge, and do so in an intuitive way. For instance did you know that

Statistical Significance Can Be Easily Understood By Rolling A Few Dice?

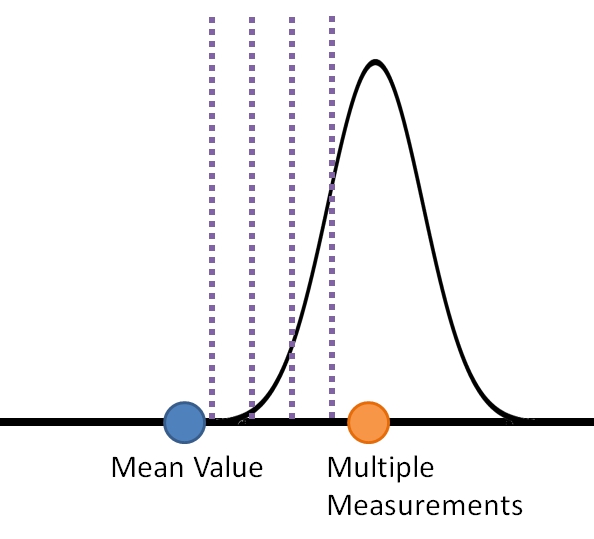
In fact, you probably already know this key concept in statistical significance, although you might not have made the connection. The concept is this. Roll a single die. Is any number more likely to come up than another ? No, they are all equally likely. Now roll 2 dice and take their sum. Suddenly the number 7 is the most likely sum (which is why casinos win on it in craps). The probability of the outcome of any single die didnt change, but the probability of the outcome of the average of all the dice rolled became more predictable. If you keep increasing the number of dice rolled, the outcome of the average gets more and more predictable. This is the exact same effect that is at the heart of all the statistical significance equations (and is explained in more detail in the book)

You Are Looking At Revision 2 Of This Book

The book that you are looking at on Amazon right now is the second revision of the book. Earlier I said that you might have missed the intuitive connections to statistical significance that you already knew. Well that is because I missed them in the first release of this book. The first release included examples for the major types of statistical significance

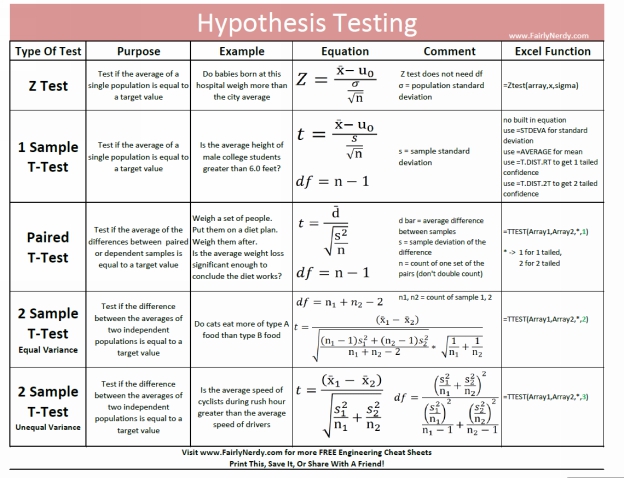
• A Z-Test
• A 1 Sample T-Test
• A Paired T Test
• A 2 Sample T-Test with equal variance
• A 2 Sample T-test with unequal variance
• Descriptions of how to use a T-table and a Z-table

And those examples were good for what they were, but were frankly not significantly different than you could find in many statistics textbooks or on Wikipedia. However this revision builds on those examples, draws connections between them, and most importantly explains concepts such as the normal curve or statistical significance in a way that will stick with you even if you dont remember the exact equation.

If you are a visual learner and like to learn by example, this intuitive booklet might be a good fit for you. Statistical Significance is fascinating topic and likely touches your life every single day. It is a very important tool that is used in data analysis throughout a wide-range of industries - so take an easy dive into the topic with this visual approach!