Since the semantics of a programming language is a relation, we will start by introducing some tools to define sets and relations.
The most basic tool is the notion of an explicit definition . We can, for example, define explicitly the function that multiplies its argument by : x 2 * x , the set of even numbers: {n | p n = 2 * p} , or the divisibility relation: {(n,m) | p n = m * p} . However, these explicit definitions are not sufficient to define all the objects we need. A second tool to define sets and relations is the notion of an inductive definition . This notion is based on a simple theorem: the fixed point theorem.
1.1.1 The Fixed Point Theorem
Let be an ordering relationthat is, a reflexive, antisymmetric and transitive relationover a set E , and let u , u , u , ... be an increasing sequence, that is, a sequence such that u u u ... The element l of E is called limit of the sequence u , u , u , ... if it is a least upper bound of the set { u , u , u , ...} , that is, if
If it exists, the limit of a sequence ( u i ) i is unique, and we denote it by lim i u i .
The ordering relation is said to be weakly complete if all the increasing sequences have a limit.
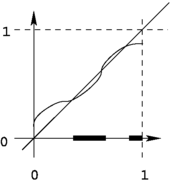
The standard ordering relation over the real numbers interval [0, 1] is an example of a weakly complete ordering. In addition, this relation has a least element . However, the standard ordering relation over + is not weakly complete since the increasing sequence 0, 1, 2, 3, ... does not have a limit.
Let A be an arbitrary set. The inclusion relation over the set (A) of all the subsets of A is another example of a weakly complete ordering. The limit of an increasing sequence U , U , U , ... is the set
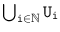
. In addition, this relation has a least element .
Let f be a function from E to E . The function f is increasing if
It is continuous if, in addition, for any increasing sequence
First Fixed Point Theorem
Let be a weakly complete ordering relation over a set E that has a least element m . Let f be a function from E to E . If f is continuous then p = lim i ( f i m) is the least fixed point of f .
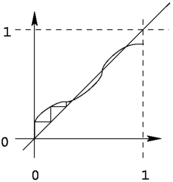
Proof
First, since m is the smallest element in E , m f m . The function f is increasing, therefore f i m f i+1 m . Since the sequence f i m is increasing, it has a limit. The sequence f i+1 m also has p as limit, thus, p = lim i (f ( f i m)) = f ( lim i ( f i m)) = f p . Moreover, p is the least fixed point, because if q is another fixed point, then m q and f i m f i q = q (since f is increasing). Hence p = lim i ( f i m) q .
The second fixed point theorem states the existence of a fixed point for increasing functions, even if they are not continuous, provided the ordering satisfies a stronger property.
An ordering over a set E is strongly complete if every subset A of E has a least upper bound sup A .
The standard ordering relation over the interval [0, 1] is an example of a strongly complete ordering relation. The standard ordering over + is not strongly complete because the set + itself has no upper bound.
Let A be an arbitrary set. The inclusion relation over the set (A) of all the subsets of A is another example of strongly complete ordering. The least upper bound of a set B is the set
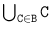
.
Exercise 1.1
Show that any strongly complete ordering is also weakly complete.
Is the ordering
weakly complete? Is it strongly complete?
Note that if the ordering over the set E is strongly complete, then any subset A of E has a greatest lower bound inf A . Indeed, let A be a subset of E , let B be the set {y E | x A y x} of lower bounds of A and l the least upper bound of B . By definition, l is an upper bound of the set B
and it is the least one
It is easy to show that l is the greatest lower bound of A . Indeed, if x is an element of A , it is an upper bound of B and since l is the least upper bound, l x . Thus, l is a lower bound of A . To show that it is the greatest one, it is sufficient to note that if m is another lower bound of A , it is an element of B and therefore m l .
The greatest lower bound of a set B of subsets of A is, of course, the set
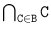
.
Second Fixed Point Theorem
Let be a strongly complete ordering over a set E . Let f be a function from E to E . If f is increasing then p = inf {c | f c c} is the least fixed point of f .
Proof
Let C be the set {c | f c c} and c be an element of C . Then p c because p is a lower bound of C . Since the function f is increasing, we deduce that f p f c . Also, f c c because c is an element of C , so by transitivity f p c .
The element f p is smaller than all the elements in C , it is therefore also smaller than or equal to its greatest lower bound: f p p .
Since the function f is increasing, f (f p) f p , thus f p is an element of C , and since p is a lower bound of C , we deduce p f p . By antisymmetry, p = f p .

![Gilles Dowek Introduction to the Theory of Programming Languages [recurso electrónico]](/uploads/posts/book/137340/thumbs/gilles-dowek-introduction-to-the-theory-of.jpg)



![Lee - Python Programming Fundamentals [recurso electrónico]](/uploads/posts/book/214321/thumbs/lee-python-programming-fundamentals-recurso.jpg)
![Hartman-Stein Paula E. - Enhancing Cognitive Fitness in Adults [recurso electrónico]: A Guide to the Use and Development of Community-Based Programs](/uploads/posts/book/212245/thumbs/hartman-stein-paula-e-enhancing-cognitive.jpg)
![Bhattacharya S K. - Epidemiological and Molecular Aspects on Cholera [recurso electrónico]](/uploads/posts/book/205862/thumbs/bhattacharya-s-k-epidemiological-and-molecular.jpg)
![Dębicki Krzysztof - Queues and Lévy Fluctuation Theory [recurso electrónico] $c](/uploads/posts/book/193156/thumbs/d-bicki-krzysztof-queues-and-l-vy-fluctuation.jpg)
![Eisner Tanja - Operator Theoretic Aspects of Ergodic Theory [recurso electrónico] $c](/uploads/posts/book/173124/thumbs/eisner-tanja-operator-theoretic-aspects-of.jpg)
![Russell - On education [recurso electrónico]](/uploads/posts/book/137691/thumbs/russell-on-education-recurso-electro-nico.jpg)

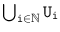 . In addition, this relation has a least element .
. In addition, this relation has a least element .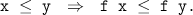
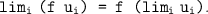

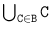 .
.
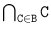 .
.