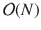1.1 Introduction
Volatility clustering, i.e. positive correlation of price variations observed on speculative markets, motivated the introduction of autoregressive conditionally heteroskedastic (ARCH) processes by Engle ().
The covariance between asset returns is of essential importance in finance. Effectively, many problems in financial theory and practice, such as asset allocation, hedging strategies or Value-at-Risk (VaR) evaluation, require some formalization not merely of univariate risk measures but rather of the entire covariance matrix (Bollerslev et al. ).
When modeling time dependent second order moments, a multivariate model is a natural framework to take cross sectional information into account. Over recent years, multivariate volatility models have been attracting high interest in econometric research and practice. Popular examples of multivariate volatility models comprise the GARCH model class recently reviewed by Bauwens et al. () while retaining its computational feasibility.
Here, we will briefly review two competing classes of MGARCH models, namely the half-vec model family and correlation models. The latter will be applied to evaluate the VaR associated with portfolios comprised by stocks listed in the Dow Jones Industrial Average (DJIA) index. We motivate the idea for VaR backtesting and reference the recent literature on (un)conditional VaR coverage tests. We compare the performance of models building on constant and dynamic conditional correlation. Moreover, it is illustrated how a univariate volatility model performs in comparison with both correlation models.
The remainder of this paper is organized as follows. The next section introduces the MGARCH model and briefly mentions some specifications that fall within the class of so-called half-vec MGARCH models. Correlation models are the focus of Sect..
1.2 Half-Vec Multivariate GARCH Models
Let
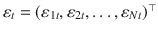
denote an N -dimensional vector of serially uncorrelated components with mean zero. The latter could be directly observed or estimated from a multivariate regression model. The process
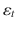
follows a multivariate GARCH process if it has the representation
where
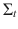
is measurable with respect to information generated up to time
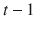
, formalized by means of the filtration
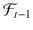
. The
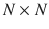
conditional covariance matrix,
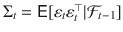
, has typical elements
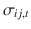
with
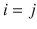
(
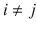
) indexing conditional variances (covariances). In a multivariate setting, potential dependencies of the second order moments in
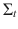
on
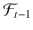
become easily intractable for practical purposes.
The assumption of conditional normality in ( ) have been derived for multivariate processes.
The so-called half-vec specification encompasses all MGARCH variants that are linear in (lagged) second order moments or squares and cross products of elements in (lagged)
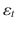
. Let vech(B) denote the half-vectorization operator stacking the elements of a
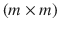
matrix B from the main diagonal downwards in a
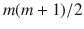
dimensional column vector. We concentrate the formalization of MGARCH models on the MGARCH(1,1) case which is, by far, the dominating model order used in the empirical literature (Bollerslev et al. ). Within the half-vec representation of the GARCH(1, 1) model
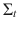
is specified as follows:
In () allows a very general dynamic structure of the multivariate volatility process. On the other hand, this specification suffers from huge dimensionality of the relevant parameter space which is of order
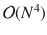
. In addition, it might be cumbersome or even impossible in applied work to restrict the admissible parameter space such that the time path of implied matrices
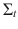
is positive definite.
To reduce the dimensionality of MGARCH models, numerous avenues have been followed that can be nested in the general class of half-vec models. Prominent examples in this vein of research are the Diagonal model (Bollerslev et al. ). The latter are assumed to exhibit volatility dynamics which are suitably modeled by univariate GARCH-type models. Thereby, factor models drastically reduce the number of model parameters undergoing simultaneous estimation. Model feasibility is, however, paid with restrictive correlation dynamics implied by the (time invariant) loading coefficients. Moreover, it is worthwhile mentioning that in case of factor specifications still
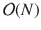












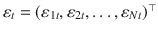 denote an N -dimensional vector of serially uncorrelated components with mean zero. The latter could be directly observed or estimated from a multivariate regression model. The process
denote an N -dimensional vector of serially uncorrelated components with mean zero. The latter could be directly observed or estimated from a multivariate regression model. The process 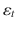 follows a multivariate GARCH process if it has the representation
follows a multivariate GARCH process if it has the representation 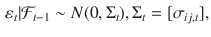
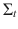 is measurable with respect to information generated up to time
is measurable with respect to information generated up to time 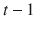 , formalized by means of the filtration
, formalized by means of the filtration 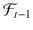 . The
. The 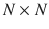 conditional covariance matrix,
conditional covariance matrix, 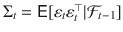 , has typical elements
, has typical elements 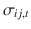 with
with 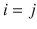 (
( 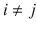 ) indexing conditional variances (covariances). In a multivariate setting, potential dependencies of the second order moments in
) indexing conditional variances (covariances). In a multivariate setting, potential dependencies of the second order moments in 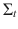 on
on 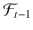 become easily intractable for practical purposes.
become easily intractable for practical purposes.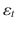 . Let vech(B) denote the half-vectorization operator stacking the elements of a
. Let vech(B) denote the half-vectorization operator stacking the elements of a 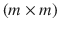 matrix B from the main diagonal downwards in a
matrix B from the main diagonal downwards in a 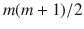 dimensional column vector. We concentrate the formalization of MGARCH models on the MGARCH(1,1) case which is, by far, the dominating model order used in the empirical literature (Bollerslev et al. ). Within the half-vec representation of the GARCH(1, 1) model
dimensional column vector. We concentrate the formalization of MGARCH models on the MGARCH(1,1) case which is, by far, the dominating model order used in the empirical literature (Bollerslev et al. ). Within the half-vec representation of the GARCH(1, 1) model 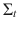 is specified as follows:
is specified as follows: 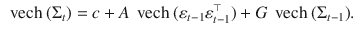
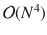 . In addition, it might be cumbersome or even impossible in applied work to restrict the admissible parameter space such that the time path of implied matrices
. In addition, it might be cumbersome or even impossible in applied work to restrict the admissible parameter space such that the time path of implied matrices 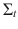 is positive definite.
is positive definite.