1. Derivatives
Classic financial mathematics deals first and foremost with basic financial instruments such as stocks, foreign currencies and bonds. A derivative ( derivative security or contingent claim ) is a financial instrument whose value depends on the value of other, more basic underlying variables. In this chapter we consider forward contracts, futures contracts and options as well as some combinations.
Simple derivatives have been known on European stock exchanges since the turn of the nineteenth century. While they lost popularity between World War I and II, they revived in the 1970s with the help of work by Black, Scholes and Merton, who developed a theoretical foundation to price such instruments. Their entrepreneurial approachwhich is not only applied to price derivatives but everywhere in finance where the risk of complex financial instruments is measured and controlled received a Nobel prize for economics in 1997. At the same time, it triggered the development of modern financial mathematics the basics of which is described in Chap. ).
Particularly simple derivative securities are forward and future contracts . Both contracts are agreements involving two parties and call for future delivery of an asset at an agreed price. Stocks, currencies and bonds, as well as agricultural products (grain, meat) and raw materials (oil, copper, electric energy) are underlying in the contract.
Definition 1.1 (Forward Contract)
A forward contract is an agreement between two parties in which one of the parties assumes a long position (the other party assumes a short position) and obliges to purchase (sell) the underlying asset at a specified future date T > t , ( expiration date or maturity ) for a specified price K ( delivery strike price ) .
At time t , the value
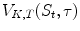
of such a contract depends on the current value of the underlying S t , the time to maturity
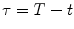
and of the parameters K , T specified in the contract.
Futures contracts closely resemble forward contracts. While the latter do not entail any further payments until maturity, once the agreement is signed, futures contracts are traded on an exchange and marked to the market on a daily basis. Under certain circumstances forward and futures prices are identical.
Example 1.1
An investor enters into a long-term forward contract on September 1, 2003, which obliges him to buy 1,000,000EUR at a specified exchange rate of 1.2USD/EUR in 90days. The investor gains if the exchange rate is up to 1.3 USD/EUR on November 30 2003, since he can sell the 1,000,000 EUR for USD 1,300,000.
In this case t = September 1, 2003 = 90days, T = November 30, and K = USD 1,200,000.
Definition 1.2 (Spot Price, Forward Price, Future Price)
The current price of the underlying (stock, currency, raw material) S t is often referred to as the spot price . The delivery price giving a forward contract a value of zero is called the forward price and denoted F t . That is, F t solves
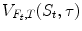
= 0. The future price is defined accordingly.
Later we will compute the value of a forward contract, which determines the forward price. Since under certain circumstances forward and future contracts have the same value, their prices are equal. When such a contract is initiated in time t =0, often the delivery price is set to K = F 0. The contract has a value of zero for both the seller and the buyer, i.e. no payments occur. Over time, as additional transactions take place on the exchange, the delivery price K and the forward price F t can be different.
Contrary to forward and futures contracts where both parties are obliged to carry out the transaction, an option gives one party the right to buy or sell the security. Obviously, its important to distinguish whether the buyer or seller of the option has the right to transact. There are two types of options: call options and put options. Furthermore, European options are delimited from American options. While European options are like forward contracts, American options can be exercised at any date before maturity. These terms are derived from historical, not geographical roots.
Definition 1.3 (Call Option, Put Option)
A European call option is an agreement which gives the holder the right to buy the underlying asset at a specified date T > t , ( expiry date or maturity ), for a specified price K , ( strike price or exercise price ). If the holder does not exercise, the option expires as worthless.
A European put option is an agreement which gives the holder the right to sell the underlying asset at a specified date T for a specified price K .
The holder of an American call or put option has the right to exercise the option at any time between t and T .
The option types defined above are also called plain vanilla options . In practice, many more complex derivatives exist and numerous new financial instruments are still emerging. Over-the-counter (OTC) derivatives are tailor made instruments designed by banking institutions to satisfy a particular consumer need. A compound option, for example, is such an OTC-derivative. It gives the holder the right to buy or sell at time T an underlying option which matures in T > T . The mathematical treatment of these exotic options is particularly difficult, since the current value of this instrument does not only depend on the value of the underlying S t but also on the entire path of the underlying,
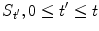
.
Asian, lookback and knock-out options are path-dependent derivatives. While the delivery price K of an Asian option depends on the average value of the security of a certain period of time, it depends, in the case of a lookback option, on the minimum or maximum value of the security for a certain period of time. Knock-out options expire as worthless if the price level ever reaches a specified level.
To get used to forward and futures contracts, plain vanilla options and simple combinations of them, it is convenient to have a look at the payoff of an instrument, i.e. the value of the derivative at maturity T . The payoff of a long position in a forward contract is just S T K , with S T the securitys spot price at expiration date T . The holder of the contract pays K for the security and can sell it for S T . Thus, he makes a profit if the value of the security S T at expiration is greater than the delivery price K . Being short in a forward contract implies a payoff K S T . Both payoff functions are depicted in Fig..
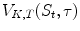 of such a contract depends on the current value of the underlying S t , the time to maturity
of such a contract depends on the current value of the underlying S t , the time to maturity 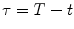 and of the parameters K , T specified in the contract.
and of the parameters K , T specified in the contract.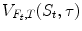 = 0. The future price is defined accordingly.
= 0. The future price is defined accordingly.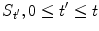 .
.












