Goriely - The Mathematics and Mechanics of Biological Growth
Here you can read online Goriely - The Mathematics and Mechanics of Biological Growth full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: New York;NY, year: 2017, publisher: Springer New York, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:The Mathematics and Mechanics of Biological Growth
- Author:
- Publisher:Springer New York
- Genre:
- Year:2017
- City:New York;NY
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
- 100
- 1
- 2
- 3
- 4
- 5
The Mathematics and Mechanics of Biological Growth: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "The Mathematics and Mechanics of Biological Growth" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Goriely: author's other books
Who wrote The Mathematics and Mechanics of Biological Growth? Find out the surname, the name of the author of the book and a list of all author's works by series.
The Mathematics and Mechanics of Biological Growth — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "The Mathematics and Mechanics of Biological Growth" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
Introduction: Where It All Starts

- Growth. The term growth by itself refers to a change in mass. It is colloquially understood as an increase in mass, but the concept extends naturally to describe mass reduction or shrinking. Change in mass can be created either by addition of mass at constant density, as found in the development of soft tissues, a change in density at constant volume, as in the case of bone densification, or both as found in a developing bone. Mathematically, a theory of growth must allow for changes in mass, volume, and density and must be flexible to account for mass permeating through the boundary of the body, accumulating at the boundary, or occurring within the body itself.
- Remodeling. It is well known that in the process of aging, tissues may become stiffer or softer. The term remodeling refers to an evolution of material properties in a system without change of mass such as stiffness, fiber orientation, fiber strength, and so forth. These remodeling processes are due to a change in the microstructure that determines the overall behavior of the tissue. For instance, the typical composition of soft tissues in many animals is a mixture of collagen fibers within an elastin matrix. Whereas elastin content remains mostly unchanged over many years, there is a continuous turnover of collagen that depends on the local biochemical and mechanical stimuli acting on the cells. The relative content of different types of collagen fibers and elastin determines the overall response of the tissue [635]. This process can occur without a change of mass, but it is crucial to understand the response of a tissue under mechanical loads. From a mathematical perspective, the variation of material properties can either be modeled by considering a separate evolution of the material parameters of a system or, at a lower scale, by taking into account the evolution of separate tissue components.
- Morphogenesis. Early in embryonic life, new tissues and organs are formed. In this process, major reorganization and differentiation of cells take place after cell division, and, importantly, there is a restructuring of material elements. This reorganization process can only happen if the adhesion between different components is weak enough so that they can separate and reattach. This simple observation has important consequences for modeling as tissues undergoing morphogenesis exhibit rapid elastic stress relaxation and plastic-like flow. Mathematically, this evolution is often described by modeling tissues as fluid or viscoelastic rather than elastic, even though these two points of views are equivalent, as we will show.
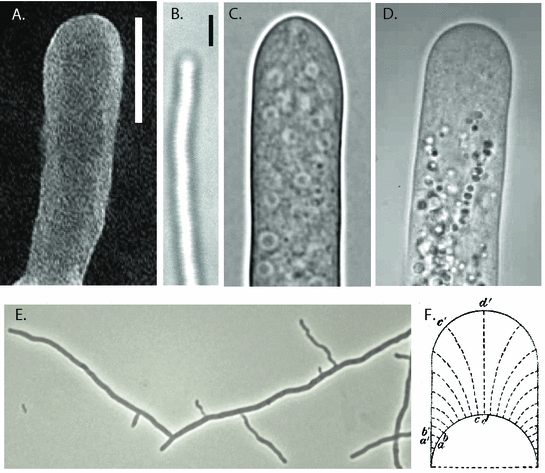
 m) ( Kitasatospora setae source: Society for Actinomycetes Japan, photograph by Y. Takahashi and Y. Iwai); B. microbacterial filament ( Streptomyces coelicolor A3(2)), (bar is 1
m) ( Kitasatospora setae source: Society for Actinomycetes Japan, photograph by Y. Takahashi and Y. Iwai); B. microbacterial filament ( Streptomyces coelicolor A3(2)), (bar is 1 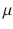 m); C. Allomyces ; D. lily root hair (typical diameter 1520
m); C. Allomyces ; D. lily root hair (typical diameter 1520 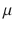 m) (images courtesy of Jacques Dumais). E. Branching in streptomyces A3(2). F. First theoretical description of tip growth by Reinhardt in 1892 for the growth of fungus [1073].
m) (images courtesy of Jacques Dumais). E. Branching in streptomyces A3(2). F. First theoretical description of tip growth by Reinhardt in 1892 for the growth of fungus [1073].Font size:
Interval:
Bookmark:
Similar books «The Mathematics and Mechanics of Biological Growth»
Look at similar books to The Mathematics and Mechanics of Biological Growth. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book The Mathematics and Mechanics of Biological Growth and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.