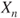Established by WALTER A. SHEWHART and SAMUEL S. WILKS
David J. Balding, Noel A. C. Cressie, Garrett M. Fitzmaurice, Harvey Goldstein, Iain M. Johnstone, Geert Molenberghs, David W. Scott, Adrian F. M. Smith, Ruey S. Tsay, Sanford Weisberg
Vic Barnett, Ralph A. Bradley, J. Stuart Hunter, J. B. Kadane, David G. Kendall, Jozef L. Teugels
A complete list of the titles in this series appears at the end of this volume.

This work is in the Wiley-Dunod Series co-published between Dunod and John Wiley Sons, Ltd.
This work is in the Wiley-Dunod Series co-published between Dunod and John Wiley & Sons, Ltd.
This edition was first published in 2014
2014 John Wiley & Sons, Ltd
Registered office
John Wiley & Sons, Ltd, The Atrium, Southern Gate, Chichester, West Sussex PO19 8SQ, United Kingdom
For details of our global editorial offices, customer services, and information about how to apply for permission to reuse the copyright material in this book, please see our web site at www.wiley.com.
The right of the author to be identified as the author of this work has been asserted in accordance with the Copyright, Designs, and Patents Act 1988.
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, except as permitted by the UK Copyright, Designs, and Patents Act 1988, without the prior permission of the publisher.
Wiley also publishes its books in a variety of electronic formats. Some content that appears in print may not be available in electronic books.
Designations used by companies to distinguish their products are often claimed as trademarks. All brand names and product names used in this book are trade names, service marks, trademarks, or registered trademarks of their respective owners. The publisher is not associated with any product or vendor mentioned in this book.
Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best efforts in preparing this book, they make no representations or warranties with respect to the accuracy or completeness of the contents of this book and specifically disclaim any implied warranties of merchantability or fitness for a particular purpose. It is sold on the understanding that the publisher is not engaged in rendering professional services and neither the publisher nor the author shall be liable for damages arising herefrom. If professional advice or other expert assistance is required, the services of a competent professional should be sought.
Library of Congress Cataloging-in-Publication Data
Graham, C. (Carl)
Markov chains : analytic and Monte Carlo computations / Carl Graham.
pages cm
Includes bibliographical references and index.
ISBN 978-1-118-51707-9 (cloth)
1. Markov processes. 2. Monte Carlo method. 3. Numerical calculations. I. Title.
QA274.7.G73 2014
519.233dc23
2013049515
A catalog record for this book is available from the British Library.
ISBN: 978-1-11851707-9
Preface
This book was born from my teaching experience in French engineering schools.In these, mathematical tools should be introduced by showing that they providemodels allowing for exact or approximate computations for relevant quantitiespertaining to realistic phenomena.
I have taught in particular a course on the Markovchains, the theory of which is already old. I had learnt a lot of it by osmosis whilestudying or doing research on more recent topics in stochastics. Teaching it forced medo delve deeper into it. This allowed me to rediscover the power and finesse ofthe probabilistic tools based on the work by Kai Lai Chung,Wolfang (or Vincent) Doeblin, Joseph Leo Doob, William Feller, and AndreiKolmogorov, which laid the ground for stochastic calculus.
I realized that Markovchain theory is actually a very active research field, both for theory and forapplications. The derivation of efficient Monte Carlo algorithms and theirvariants, for instance adaptive ones, is a hot subject, and often these are theonly methods allowing tractable computations for treating the enormousquantities of data that scientists and engineers can now acquire. This neednotably feeds theoretical studies on long-time rates of convergence for Markovchains.
This book is aimed at a public of engineering school and masterstudents and of applied scientists and engineers, wishing to acquire thepertinent mathematical bases. It is structured and animated by a few classicexamples, which are each investigated at different stages of the book andeventually studied exhaustively. These illustrate in real time the newly introducednotions and their qualitative and quantitative uses. It also elaborates on thegeneral matter of Monte Carlo approximation.
This book owes a lot tothe forementioned mathematicians, as well as the authors ofthe too small bibliography. More personal contributions to this book were provided by discussions with other teachers and researchers and by theinteraction with the students, notably those in the engineering schools withtheir pragmatic perspective on mathematics.
Feller's book [3] has alwaysimpressed me, notably by the wealth of examples of a practical nature itcontains. It represents a compendium of probability theory at his time and canreadily be adapted to a modern public. Reading it has lead me to try topush some explicit computations quite far, notably using generatingfunctions, but my efforts are pale with respect to his achievements in thisperspective.
List of Figures
| 1.1 | Symmetric nearest-neighbor random walk on regular planar triangular network. |
| 1.2 | Gambler's ruin. Gambler A finishes the game at time 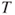 with a gain of with a gain of 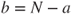 units starting from a fortune of units starting from a fortune of 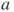 units. The successive states of his fortune are represented by the and joined by dashes. The arrows on the vertical axis give his probabilities of winning or losing at each toss. units. The successive states of his fortune are represented by the and joined by dashes. The arrows on the vertical axis give his probabilities of winning or losing at each toss. |
| 1.3 | Branching process. (b) The genealogical tree for a population during six generations; represent individuals and dashed lines their parental relations. (a) The vertical axis gives the numbers 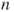 of the generations, of which the sizes figure on its right. (c) The table underneath the horizontal axis gives the of the generations, of which the sizes figure on its right. (c) The table underneath the horizontal axis gives the 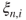 for for 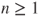 and and 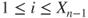 , of which the sum over , of which the sum over 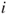 yields yields 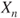 |














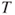 with a gain of
with a gain of 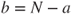 units starting from a fortune of
units starting from a fortune of 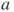 units. The successive states of his fortune are represented by the and joined by dashes. The arrows on the vertical axis give his probabilities of winning or losing at each toss.
units. The successive states of his fortune are represented by the and joined by dashes. The arrows on the vertical axis give his probabilities of winning or losing at each toss.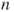 of the generations, of which the sizes figure on its right. (c) The table underneath the horizontal axis gives the
of the generations, of which the sizes figure on its right. (c) The table underneath the horizontal axis gives the 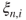 for
for 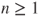 and
and 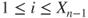 , of which the sum over
, of which the sum over 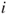 yields
yields