Introduction
The method of autonomous orbit determination using magnetic measurement information generally uses the extended Kalman filter (Extended Kalman, Filter, EKF), in addition to the unscented Kalman filter (Unscented Kalman Filter, UKF) to confirm satellite position and velocity, and they are based on the assumption that the distribution of state variables is similar to the Gauss distribution, and estimate the mean and covariance of state variables []. When the distributions of the state variables were not Gauss distribution, the performance of the filter algorithm will be reduced, even if the initial position and velocity distribution are Gauss distribution, but the process noise and the measurement noise are white Gauss noise. At this time, because of the nonlinearity in the model, the actual distribution of position and velocity is not Gauss distribution. In order to solve the nonlinear model and the estimation of the initial deviation to the negative effects caused by the filtering, this paper uses particle filtering algorithm for satellite orbit, and its effectiveness is proved by mathematical simulation.
Particle Filter Algorithm and Orbit Estimation
The particle filter is used for target tracking, and its principle is that the particle filter (Particle Filter PF) is a kind of approximate Bayesian filtering algorithm [].
The basic problem of the orbit determination is as follows: The dynamic process of a differential equation is not exactly known, and the optimal estimation of the motion state of the satellite in a certain sense is solved using the observation value with error and the not accurate initial state. When the system can be described as a linear model, and the system and the measurement error are white noise, the unbiased optimal estimation in statistical sense can be obtained by Kalman filtering []. However, in practical applications, the target motion model and the measurement model are mostly nonlinear; the noise is non-Gauss; and the traditional Kalman filter application has been limited. Relative orbit determination problem is usually based on the Hill equation using extended Kalman filtering algorithm to estimate the state of the target aircraft. Because of the need to linearize the state equation and the Hill equation which is only applicable to the relative distance filtering calculation, when the relative distance or large initial errors are easy to cause filter divergence and its application scope has been greatly constrained, therefore, the application to the relative distance between the target orbit determination method will be an important direction for future research.
With the development of space technology, the requirement of spacecraft orbit precision becomes higher and higher. The data processing methods of satellite orbit determination can be divided into two categories: (1) batch processing. Using all data to get track and related parameter of the epoch is a method of post-processing, needs to store a large number of observation value, and demands high processing ability of computer. (2) Sequential recursive method. When the observation value is reached, the corresponding processing is performed, and the next moment is no longer observed by the previous moment. The particle filter algorithm is a sequential recursive method; the data processing only uses the current value of observation data and the previous data storage, and requires lower capacity of the computer. The particle filter algorithm for solving nonlinear and non-Gauss problems has obvious theoretical advantages, such as the algorithm can be used to set orbit spacecraft, which is bound to improve the accuracy of orbit determination. However, no one shows any interest in the research model, algorithm, and application of the precise orbit of the spacecraft.
Satellite Orbit Determination Model Based on Particle Filter
3.1 Satellite Orbit Influence Factor Analysis
The satellite is subjected to various forces in the course of the movement around the earth; these forces can be divided into two categories: one is conservative forces; the other is the divergent force []. Conservative forces include earth gravity, day, month, the gravity of the planet to the satellite, and the gravitational field changes caused by the earth tide phenomenon. For conservative force systems, it can be described by the bit function. The divergence force includes the atmospheric resistance, the earth infrared radiation, and the power of satellite attitude control. The divergence force does not have the position function, so the expression is directly used. The expressions of the above forces are very complex. Besides the two-body problem, it is difficult to obtain the analytical solution of the motion equation of the satellite, which is usually based on the approximate analytical solution.
On orbit determination, dynamic model is not very accurate. The main point is as follows: Under certain accuracy, dynamic model omits some perturbed factors, even without omission, it also made some simplifications and approximations. In the considered perturbation factors, the model parameters are approximate. The initial state of general satellite
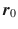
and
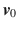
could not be precisely known; only the reference value
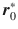
and
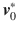
needs to continue to refine the satellite observation reference value in order to obtain the initial motion state
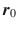
and
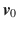
of satellite. Measurement data itself are not very accurate; the equipment itself and a variety of factors affect measurement data with random error and system error. Therefore, the orbit estimation problem is a dynamic process which is not known exactly for the differential equation, and the best estimate of the satellite motion state is obtained using the observational data with random errors and the inaccurate initial state.













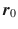 and
and 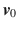 could not be precisely known; only the reference value
could not be precisely known; only the reference value 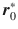 and
and 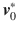 needs to continue to refine the satellite observation reference value in order to obtain the initial motion state
needs to continue to refine the satellite observation reference value in order to obtain the initial motion state 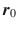 and
and 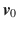 of satellite. Measurement data itself are not very accurate; the equipment itself and a variety of factors affect measurement data with random error and system error. Therefore, the orbit estimation problem is a dynamic process which is not known exactly for the differential equation, and the best estimate of the satellite motion state is obtained using the observational data with random errors and the inaccurate initial state.
of satellite. Measurement data itself are not very accurate; the equipment itself and a variety of factors affect measurement data with random error and system error. Therefore, the orbit estimation problem is a dynamic process which is not known exactly for the differential equation, and the best estimate of the satellite motion state is obtained using the observational data with random errors and the inaccurate initial state.