Daniele Mundici UNITEXT Logic: A Brief Course 10.1007/978-88-470-2361-1_1 Springer-Verlag Italia 2012
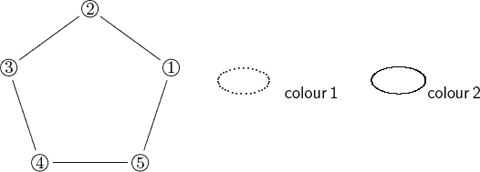
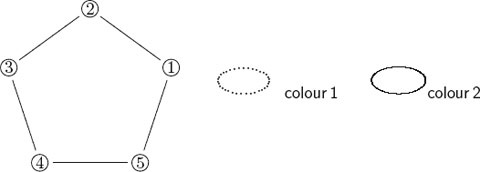
Have a look at the following drawing:
The problem C is to colour the vertices 1, ...,5 with one of two available colours, in such a way that vertices of the same edge have different colours. The answer is simple, but think of the same problem, denoted by C +, to colour a complex graph with 1000 vertices, 10000 edges and a palette of 7 colours. The search for efficient methods of solving a problem like C +, so either finding an explicit solution or proving that no solution exists, forms a central challenge for contemporary mathematics.
Working hypothesis . A Martian announces the solution to problems C and C + .
The unknowns, or variables, of the problem are the questions that we would ask the Martian to solve the problem ourselves. The questions have to be binary, in the sense that the answer can be only yes or no. A question of the type How many vertices have you coloured with the first colour is not admissible. Rather, the only questions that are admissible are of the form:
Have you coloured vertex 4 with colour number 2?
For brevity we will write X instead of writing this question out in English. We will consider only the problem C . The answers to the complete bundle of questions X ij ( i = 1, 2, 3,4, 5; j = 1 , 2) allow us to extract the solution that the Martian claims to have.
For the problem C + there are 7000 unknowns X ij . So each X ij is a symbolic expression that expects an answer 1 (namely yes) or 0 (namely no) from the Martian. In mathematics one gives to such neither fish nor fowl expressions the name unknowns or variables, to emphasise the fact that when posing the question we do not know the answer. Here there are two possible answers that depend on the solution. In traditional mathematical practice the variables and the unknowns often represent rational, real or complex numbers. Here instead, each unknown represents a bit (binary digit ) that will get one of two values, 0 or 1.
The question X ij , when we omit the question mark, becomes the statement vertex i is coloured with colour number j . As such it can be negated and transformed into the statement vertex i is not coloured with colour number j , that we will abbreviate writing X ij . These elementary statements X ij and their negations X i j are called literals of the problem. Operating on our 20 literals with disjunction and conjunction , the graph colouring problem C is completely rewritten as a system, that is, a conjunction, of simple equations in the unknowns X ij . Each equation has the form of a disjunction of the variables X ij or the negated variables X ij . In Table () one finds a transcribed system of equations associated with the problem C , with an informal commentary on the meaning of each symbolic expression.
This long rigmarole is not an example of good English prose, but it has the merit of showing that each graph colouring problem, such as C or C + , can be completely described by a few rudimentary linguistic instruments: the variables and their negations, the connective or and the connective and, the latter tacitly represented by the long brace. Since the Martian understands only this language, and answers in monosyllables (bits), perhaps studying this system of equations and realising that it has no solution, he will reconsider his announcement.
In the first part of this course we will study how to decide mechanically whether a system of this type has a solution and, in case it does, how to compute at least one. Each possible solution of the system () provides sufficient information on how to colour the pentagon so that all the required conditions are satisfied.
And in fact, with a calculation given on page 29, we will verify that system () is unsatisfiable, which corresponds to the impossibility of colouring the pentagon with two colours in such a way that the vertices of the same edge have different colours. The same type of calculation will allow us to decide whether the analogous problem C + has a solution. The calculation may appear useless for the trivial problem C , but it becomes an essential instrument in solving, at least in principle, formidable problems such as C +. Up till now no shortcuts have been found to solve the graph colouring problems.
Appreciation of logic dawns upon us with the realisation of the fact that in formula (). For a problem more difficult, like C +, the same type of translation may provide the crucial step in obtaining a solution. As we will see, the significance of these systems goes well beyond the graph colouring problems: they are interesting objects of study, independently of the problem they represent.
Also the systems of linear equations have similar characteristics, to the point that nowadays the solvers of such systems are predominantly computer programs and not mathematicians. In logic the unknowns do not represent real numbers, but statements, which are immediate products of thought and language. Therefore to solve these systems special manipulations will be necessary, a calculus of reasoning (calculus ratiocinator in Latin).
The following table-vocabulary shows the link between problems such as C + and the main concepts of mathematical logic that we will study in the next chapters.
The colouring problem | Its formalization |
question | variable X |
answers no, yes | truth values 0,1 |
elementary assertion, its negation | literal L |
equation | clause C |
system of equations for the problem | CNF formula F |
a bundle of answers | assignment |
a bundle of answers solves the problem | satisfies F |
there does not exist a solution to the problem | F is unsatisfiable |
there exists a solution to the problem | F is satisfiable |
Daniele Mundici UNITEXT Logic: A Brief Course 10.1007/978-88-470-2361-1_2 Springer-Verlag Italia 2012
2. Fundamental Logical Notions