• Complain
LitArk » Books » Home and family

Radhakrishnan Nagarajan Marco Scutari - Bayesian networks in R: with applications in systems biology

Here you can read online Radhakrishnan Nagarajan Marco Scutari - Bayesian networks in R: with applications in systems biology full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: New York, year: 2013, publisher: Springer New York, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:

Romance novel Science fiction Adventure Detective Science History Home and family Prose Art Politics Computer Non-fiction Religion Business Children Humor

Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.

Radhakrishnan Nagarajan Marco Scutari Bayesian networks in R: with applications in systems biology

Bayesian networks in R: with applications in systems biology: summary, description and annotation

We offer to read an annotation, description, summary or preface (depends on what the author of the book "Bayesian networks in R: with applications in systems biology" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.

Introduction -- Bayesian Networks in the Absence of Temporal Information -- Bayesian Networds in the Presence of Temporal Information -- Bayesian Network Inference Algorithms -- Parallel Computing for Bayesian Networks -- Solutions -- Index -- References.;Bayesian Networks in R with Applications in Systems Biology introduces the reader to the essential concepts in Bayesian network modeling and inference in conjunction with examples in the open-source statistical environment R. The level of sophistication is gradually increased across the chapters with exercises and solutions for enhanced understanding and hands-on experimentation of key concepts. Applications focus on systems biology with emphasis on modeling pathways and signaling mechanisms from high throughput molecular data. Bayesian networks have proven to be especially useful abstractions in this regards as exemplified by their ability to discover new associations while validating known ones. It is also expected that the prevalence of publicly available high-throughput biological and healthcare data sets may encourage the audience to explore investigating novel paradigms using the approaches presented in the book.

Radhakrishnan Nagarajan Marco Scutari: author's other books


Who wrote Bayesian networks in R: with applications in systems biology? Find out the surname, the name of the author of the book and a list of all author's works by series.


Radhakrishnan Nagarajan Marco Scutari - Bayesian networks in R: with applications in systems biology
Bayesian networks in R: with applications in systems biology
Radhakrishnan Nagarajan Marco Scutari
Bayesian networks in R: with applications in systems biology

Bayesian networks in R: with applications in systems biology — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Bayesian networks in R: with applications in systems biology" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓
↑
Reset

Interval:

↓
↑

Bookmark:

Make
1234567...48
Radhakrishnan Nagarajan , Marco Scutari and Sophie Lbre Use R! Bayesian Networks in R 2013 with Applications in Systems Biology 10.1007/978-1-4614-6446-4_1 Springer Science+Business Media New York 2013
1. Introduction
Radhakrishnan Nagarajan 1, Marco Scutari 2 and Sophie Lbre 3
(1)
Division of Biomedical Informatics Department of Biostatistics, University of Kentucky, Lexington, Kentucky, USA
(2)
Genetics Institute, University College London, London, UK
(3)
ICube, Universit de Strasbourg, Strasbourg, France
Abstract
Bayesian networks and their applications to real-world problems lie at the intersection of several fields such as probability and graph theory. In this chapter a brief introduction to the terminology and the basic properties of graphs, with particular attention to directed graphs, is provided. As with other Use R!-series books, a brief introduction to the R environment and basic R programming is also provided. Some background in probability theory and programming is assumed. However, the necessary references are included under the respective sections for a more complete treatment.
1.1 A Brief Introduction to Graph Theory
1.1.1 Graphs, Nodes, and Arcs
A graph G =( V , A ) consists of a nonempty set V of nodes or vertices and a finite (but possibly empty) set A of pairs of vertices called arcs , links , or edges .
Each arc a =( u , v ) can be defined either as an ordered or an unordered pair of nodes, which are said to be connected by and incident on the arc and to be adjacent to each other. Since they are adjacent, u and v are also said to be neighbors . If ( u , v ) is an ordered pair, u is said to be the tail of the arc and v the head ; then the arc is said to be directed from u to v and is usually represented with an arrowhead in v ( u v ). It is also said that the arc leaves or is outgoing for u and that it enters or is incoming for v . If ( u , v ) is unordered, u and v are simply said to be incident on the arc without any further distinction. In this case, they are commonly referred to as undirected arcs or edges , denoted with e E and represented with a simple line ( u v ).
The characterization of arcs as directed or undirected induces an equivalent characterization of the graphs themselves, which are said to be directed graphs (denoted with G =( V , A )) if all arcs are directed, undirected graphs (denoted with G =( V , E )) if all arcs are undirected, and partially directed or mixed graphs (denoted with G =( V , A , E )) if they contain both directed and undirected arcs.
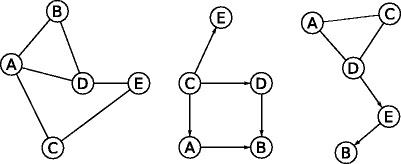
Examples of directed , undirected , and mixed partially directed graphs are shown in Fig.:
  • The node set is V ={ A,B,C,D,E} and the edge set is E ={ (AB), (AC), (AD), (BD), (CE), (DE) }.
  • Arcs are undirected, so, i.e., AB and BA are equivalent and identify the same edge.
  • Likewise, A is connected to B, B is connected to A, and A and B are adjacent.
Fig 11 An undirected graph left a directed graph center and a - photo 1
Fig. 1.1
An undirected graph ( left ), a directed graph ( center ) and a partially directed graph ( right )
For the directed graph, Fig :
  • The node set is V ={ A,B,C,D,E} and the graph is characterized by an arc set A ={ (A B), (CA), (DB), (CD), (C E)} instead of an edge set E .
  • Arcs are directed, so, i.e., AB and BA identify different arcs. For instance, AB A while BA A . Under the additional constraint of acyclicity, it is not possible for both arcs to be present in the graph because there can be at most one arc between each pair of nodes.
  • Also, A and B are adjacent, as there is an arc (AB) from A to B. AB is an outgoing arc for A (the tail), an incoming arc for B (the head), and an incident arc for both A and B.
On the other hand, the partially directed graph, Fig., is characterized by the combination of an edge set E ={ (A C), (AD), (C D)} and an arc set A ={ (D E), (E B)}.
An undirected graph can always be constructed from a directed or partially directed one by substituting all the directed arcs with undirected ones; such a graph is called the skeleton or the underlying undirected graph of the original graph.
1.1.2 The Structure of a Graph
The pattern with which the arcs appear in a graph is referred to as either the structure of the graph or the configuration of the arcs. In the context of this book it is assumed that the vertices u and v incident on each arc are distinct and that there is at most one arc between them so that ( u , v ) uniquely identifies an arc. This definition also implicitly excludes presence of a loop that can occur when u = v .
The simplest structure is an empty graph , i.e., a graph with no arcs. On the other end of the spectrum are saturated graphs , in which each node is connected to every other node. Real-world graphical abstractions usually fall between these two extremes and can be either sparse or dense . 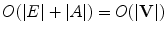While the distinction between these two classes of graphs is rather vague, a graph is usually considered sparse if Bayesian networks in R with applications in systems biology - image 2 .
The structure of a graph can reveal interesting statistical properties. Some of the most important ones deal with paths . Paths are essentially sequences of arcs or edges connecting two nodes, called end-vertices or end-nodes . Paths are denoted with the sequence of vertices ( v 1, v 2,, v n ) incident on those arcs. The arcs connecting the vertices v 1, v 2,, v n are assumed to be unique, so that a path passes through each arc only once. In directed graphs it is also assumed that all the arcs in a path follow the same direction, and we say that a path leads fromv 1 (i.e., the tail of the first arc in the path) tov n (i.e., the head of the last arc in the path). In undirected and mixed graphs (and in general when referring to a graph regardless which class it belongs to), arcs in a path can point in either direction or be undirected. Paths in which v 1= v n are called cycles and are treated with particular care in Bayesian network theory.
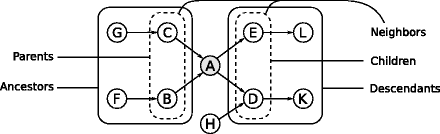
The structure of a directed graph defines a partial ordering of the nodes if the graph is acyclic , that is, if it does not contain any cycle or loop. This ordering is called an acyclic or topological ordering and is induced by the direction of the arcs. It is defined as follows: if a node v i precedes v j , there can be no arc from v j to v i . According to this definition the first nodes are the root nodes , which have no incoming arcs, and the last ones are the leaf nodes , which have at least one incoming arc but no outgoing ones. Furthermore, if there is a path leading from v i to v j , v i precedes v j in the sequence of the ordered nodes. In this case v i is called an ancestor of v j and v j is called a descendant of v i . If the path is composed by a single arc, by analogy x i is a parent of v j and v j is a child of v i .
Consider, for instance, node A in the directed acyclic graph shown in Fig.. Its neighborhood is the union of the parents and children; adjacent nodes necessarily fall into one of these two categories. Its parents are also ancestors, as they necessarily precede A in the topological ordering. Likewise, children are also descendants.
Fig 12 Parents children ancestors descendants and neighbors of node A in - photo 3
Next page
1234567...48
Light

Font size:

↓
↑
Reset

Interval:

↓
↑

Bookmark:

Make

Similar books «Bayesian networks in R: with applications in systems biology»

Look at similar books to Bayesian networks in R: with applications in systems biology. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.


Quan Nguyen - Bayesian Optimization in Action (MEAP V7)
Bayesian Optimization in Action (MEAP V7)
Quan Nguyen
Bayesian Optimization in Action (MEAP V7)
No cover
No cover
Hemachandran K
Bayesian Reasoning and Gaussian Processes for Machine Learning Applications
No cover
No cover
Sergios Theodoridis
Machine Learning: A Bayesian and Optimization Perspective
No cover
No cover
Anthony OHagan
The Oxford Handbook of Applied Bayesian Analysis (Oxford Handbooks)
Nick Heard - An Introduction to Bayesian Inference, Methods and Computation
An Introduction to Bayesian Inference, Methods and Computation
Nick Heard
An Introduction to Bayesian Inference, Methods and Computation
Lucas Pinheiro Cinelli - Variational Methods for Machine Learning with Applications to Deep Networks
Variational Methods for Machine Learning with Applications to Deep Networks
Lucas Pinheiro Cinelli
Variational Methods for Machine Learning with Applications to Deep Networks
No cover
No cover
Osvaldo Martin
Bayesian Analysis with Python
Watanabe Shinji - Bayesian speech and language processing
Bayesian speech and language processing
Watanabe Shinji
Bayesian speech and language processing
Chi Yau - R Tutorial with Bayesian Statistics Using OpenBUGS
R Tutorial with Bayesian Statistics Using OpenBUGS
Chi Yau
R Tutorial with Bayesian Statistics Using OpenBUGS
Dr. Hari M. Koduvely - Learning Bayesian Models with R
Learning Bayesian Models with R
Dr. Hari M. Koduvely
Learning Bayesian Models with R
Cameron Davidson-Pilon - Bayesian Methods for Hackers
Bayesian Methods for Hackers
Cameron Davidson-Pilon
Bayesian Methods for Hackers
No cover
No cover
Gudmund R. Iversen
Bayesian statistical inference
Reviews about «Bayesian networks in R: with applications in systems biology»

Discussion, reviews of the book Bayesian networks in R: with applications in systems biology and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.