Supplements
Path integration now enjoys a central role in many areas of physics and chemistry. Its impact has been felt in other fields as well. For example, in seismology the path integral provides a way to deal with partial differential equations, while for finance it is a tool for the analysis of stochastic processes.
With the issuing of this Dover Edition, I am adding a few new topics. They are presented in Sec. I of this supplement. While some are elementary and hopefully of broad interest, I am not providing a comprehensive survey of developments, as might be suitable for a bona fide second edition (which this is not). The coverage ranges from self-contained to telegraphic. Sec. II lists recent texts where a fuller picture can be obtained. Finally, in Sec. III are errata and comments on particular parts of this book. Partly these are factors of two and such (which eluded me, despite the opportunity to correct them on each of Wileys dozen or so reprintings), but mainly they are comments that were too lengthy to fit on the reprinted page.
References to Sections 1 through 32 are to sections of this book (a.k.a. chapters). Similarly, equation numbers with periods, ( n.m ), refer to equations in the book, while those consisting of a number alone refer to the supplement. Sections of the supplement have labels beginning with Roman numerals.
In preparing this supplement I have had the help of many individuals. Moreover, since the publication of the book, quite a few people have come to me with corrections, some of which were incorporated in previous reprintings and some of which appear here. Since these events stretch over 20 years, I hope those whose contributions have slipped my mind will forgive me. Those I recalland thank, whether for counsel, corrections or bothare A. Auerbach, Y. Avron, C. Dewitt, P. Exner, P. Facci, B. Gaveau, H. Grabert, T. Jacobson, H. Jauslin, G. Junker, M. Kac, S. Kivelson, A. Mann, D. McLaughlin, E. Mihokova, D. Mozyrsky, D. Mugnai, S. Pascazio, P. Pechukas, A. Ranfagni, M. Revzen, G. Roepstorff, M. Roncadelli, A. Scardicchio, L. J. Schulman, D. Tolkunov, U. Weiss, and N. Yamada.
Contents
- I. Topical supplements
- Path integral in a magnetic field using the Trotter product formula
- Splitting a sum
- Splitting a product
- A more accurate product formula
- Precision and rough paths
Notes
- Path decomposition expansion
- The formula
- Proof of the path decomposition expansion
- More than one dimension
Notes
- Checkerboard path integral
Notes
- Exact solutions
- -function path integral
- Half-plane barrier
- Coulomb potential and related solutions
Notes
- Dissipation and other forced-oscillator applications
- Mathematical developments
- Electromagnetism and other PDEs
- Homotopy
- And more...
- Variational corrections to the classical partition function
- A particular numerical approach
- Semiclassical approximations for coherent states
- Chaos and order
- II. Literature
- Texts and review articles
- Conference proceedings
- III. Page by page comments and errata
References and endnotes for the supplements
I. TOPICAL SUPPLEMENTS
A. Path integral in a magnetic field using the Trotter product formula
In Sec. 1 the path integral is derived using the Trotter product formula. This is basically the statement
where standard notation, H = p 2 / 2m + V, etc., is used. Later, in Sec. 4, I turn to a more delicate derivation, the path integral in the presence of a magnetic field. This involves a term 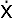
 A in the classical Lagrangian and, as explained in Sec. 5, to the need to evaluate A (x) at the midpoints along the broken line path within a path integral.
A in the classical Lagrangian and, as explained in Sec. 5, to the need to evaluate A (x) at the midpoints along the broken line path within a path integral.
The derivation in Sec. 4 follows the original paper of Feynman. However, by a slight modification of the method of Sec. 1, it is possible to use the Trotter formula. The yet more delicate case of a curved-space metric can also be treated by operator methods.
1. Splitting a sum
As usual, we want the propagator, G, the kernel of the operator exp( -iHt/ 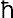 ). With a magnetic field
). With a magnetic field
where A is the vector potential. For a , b R3, G satisfies the following sequence of identities
where after line (3) I use the definition t/N . Eq. (3-4) can be written concisely as
with x N = b , and x 0 = a . This is the starting point for the Sec. 1 derivation. The smallness of allowed H to be split into kinetic and potential energy terms. For convergence one must maintain O() accuracy. That is, G ( x 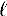 +1, ; x
+1, ; x 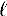 ) can be replaced by other functions that differ only by terms going to zero faster than . For numbers this can be seen by recalling that [1 + ( x + a N) / N ] N e x provided a N 0. For operators this is a more nuanced project and the reader is referred to Sec. 1 and its Notes.
) can be replaced by other functions that differ only by terms going to zero faster than . For numbers this can be seen by recalling that [1 + ( x + a N) / N ] N e x provided a N 0. For operators this is a more nuanced project and the reader is referred to Sec. 1 and its Notes.
The goal then is to approximate G ( x, ; y ) to first order in . It is helpful to phrase this in operator language. For operators A and B ,
The propagator is of this form, with = , A = - iK / 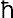 , B = - iV/
, B = - iV/ 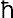 , and K the kinetic energy (called T in Sec. 1). For present purposes it is sufficient to know that
, and K the kinetic energy (called T in Sec. 1). For present purposes it is sufficient to know that














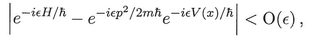
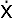
 A in the classical Lagrangian and, as explained in Sec. 5, to the need to evaluate A (x) at the midpoints along the broken line path within a path integral.
A in the classical Lagrangian and, as explained in Sec. 5, to the need to evaluate A (x) at the midpoints along the broken line path within a path integral.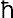 ). With a magnetic field
). With a magnetic field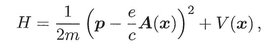
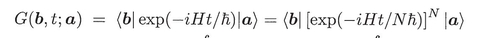
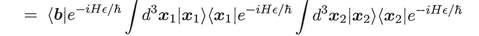
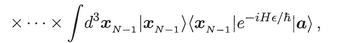
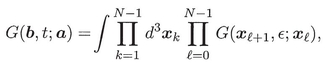
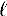 +1, ; x
+1, ; x