John Heading - An Introduction to Phase-Integral Methods
Here you can read online John Heading - An Introduction to Phase-Integral Methods full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2013, publisher: Dover Publications, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:An Introduction to Phase-Integral Methods
- Author:
- Publisher:Dover Publications
- Genre:
- Year:2013
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
An Introduction to Phase-Integral Methods: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "An Introduction to Phase-Integral Methods" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Since the number of applications is vast, the text considers only a brief selection of topics and emphasizes the method itself rather than detailed applications. The process, once derived, is shown to be one of essential simplicity that involves merely the application of certain well-defined rules. Starting with a historical survey of the problem and its solutions, subjects include the Stokes phenomenon, one and two transition points, and applications to physical problems. An appendix and bibliography conclude the text.
John Heading: author's other books
Who wrote An Introduction to Phase-Integral Methods? Find out the surname, the name of the author of the book and a list of all author's works by series.














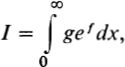 the convergence of the integral being assumed.
the convergence of the integral being assumed. 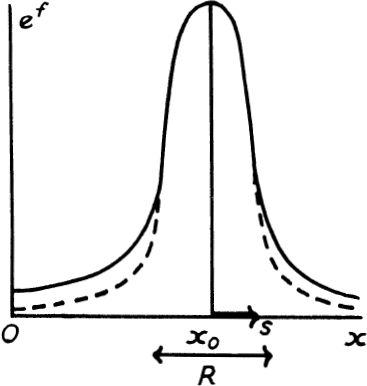 FIG. 35 We replace the hump (usually formed by a non-integrable function) by a similar hump (formed by an integrable function), the two curves differing only appreciably for values of x outside R.
FIG. 35 We replace the hump (usually formed by a non-integrable function) by a similar hump (formed by an integrable function), the two curves differing only appreciably for values of x outside R. 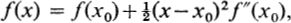 where (x0) is negative for a maximum. If xx0 = s, and if g(x) is replaced by g(x0) throughout R, we have approximately
where (x0) is negative for a maximum. If xx0 = s, and if g(x) is replaced by g(x0) throughout R, we have approximately 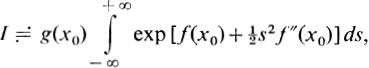 where the limits are used in order to facilitate the integration. In the figure, the dotted line represents the curve under which we are calculating the area. If
where the limits are used in order to facilitate the integration. In the figure, the dotted line represents the curve under which we are calculating the area. If 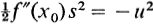 , we have
, we have 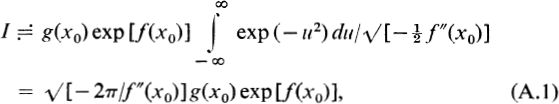 using the standard infinite integral exp ( u2) du = . This technique is a simplification of the method known as the method of steepest descents in the complex plane.
using the standard infinite integral exp ( u2) du = . This technique is a simplification of the method known as the method of steepest descents in the complex plane.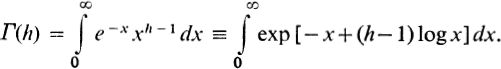 The graph of the integrand when h is large consists of a tall narrow peak.
The graph of the integrand when h is large consists of a tall narrow peak. 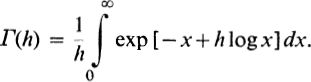 , we have f(x) = x + h log x, f(x) = 1 + h/ x, f(x) = h/ x2. f(x) vanishes when x = h, so f(h) = h + h log h and f(h) = 1/ h; when h is large, the third derivative would be negligible. Equation () now gives
, we have f(x) = x + h log x, f(x) = 1 + h/ x, f(x) = h/ x2. f(x) vanishes when x = h, so f(h) = h + h log h and f(h) = 1/ h; when h is large, the third derivative would be negligible. Equation () now gives 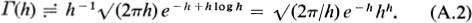 This approximation is known as Stirling's formula. If h is complex, such that < arg h < , a more complete defini-tion of (h) is required, but the same approximate formula is valid, provided arg h lies within this restricted range.
This approximation is known as Stirling's formula. If h is complex, such that < arg h < , a more complete defini-tion of (h) is required, but the same approximate formula is valid, provided arg h lies within this restricted range.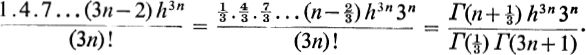 We therefore consider the continuous graph
We therefore consider the continuous graph 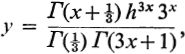 the area under the graph for positive x being the approximate sum of the series w1. The individual terms in w1 (and hence the value of y) . When x is large, the use of formula () yields
the area under the graph for positive x being the approximate sum of the series w1. The individual terms in w1 (and hence the value of y) . When x is large, the use of formula () yields 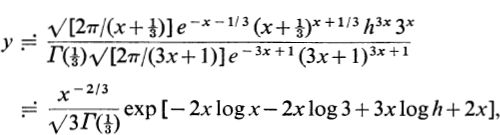 where x2/3 is a slowly varying function contrasted to the exponent of the exponential.
where x2/3 is a slowly varying function contrasted to the exponent of the exponential.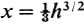 at which point
at which point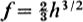 and f = 6 h3/2. Hence, using formula (), we obtain
and f = 6 h3/2. Hence, using formula (), we obtain 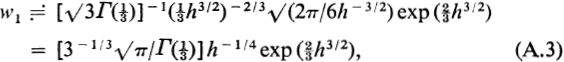 a dominant expansion. This is one of the W.K.B.J. solutions of the Airy equation, but with a definite numerical coefficient. Similarly, w2 is replaced by
a dominant expansion. This is one of the W.K.B.J. solutions of the Airy equation, but with a definite numerical coefficient. Similarly, w2 is replaced by 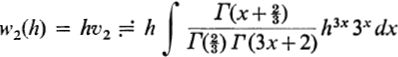 where again h is real, large and positive.
where again h is real, large and positive. 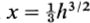 yielding
yielding 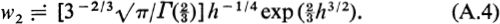 Two standard tabulated solutions [] are taken to be
Two standard tabulated solutions [] are taken to be 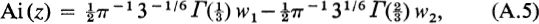
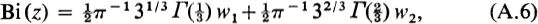 for reasons now to be discussed. ) must be subdominant along the positive real axis; this method does not however produce the subdominant expression. Similarly, substitution into () yields after simplification
for reasons now to be discussed. ) must be subdominant along the positive real axis; this method does not however produce the subdominant expression. Similarly, substitution into () yields after simplification