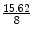Part 1
Acquisition of Diffusion MRI
Thomas Schultz , Gemma Nedjati-Gilani , Archana Venkataraman , Lauren O'Donnell and Eleftheria Panagiotaki (eds.) Mathematics and Visualization Computational Diffusion MRI and Brain Connectivity 2014 MICCAI Workshops, Nagoya, Japan, September 22nd, 2013 10.1007/978-3-319-02475-2_1
Springer International Publishing Switzerland 2014
Comparing Simultaneous Multi-slice Diffusion Acquisitions
Yogesh Rathi 1
(1)
Brigham and Womens Hospital, Harvard Medical School, Boston, MA, USA
(2)
Boston Childrens Hospital, Harvard Medical School, Boston, MA, USA
(3)
Massachusetts General Hospital, Harvard Medical School, Boston, MA, USA
Yogesh Rathi (Corresponding author)
Email:
Abstract
Diffusion magnetic resonance imaging (dMRI) is an important tool that allows non-invasive investigation of the neural architecture of the brain. Advanced dMRI protocols typically require a large number of measurements for accurately tracing the fiber bundles and estimating the diffusion properties (such as, FA). However, the acquisition time of these sequences is prohibitively large for pediatric as well as patients with certain types of brain disorders (such as, dementia). Thus, fast echo-planar imaging (EPI) acquisition sequences were proposed by the authors in [6, 16], which acquired multiple slices simultaneously to reduce scan time. The scan time in such cases drops proportionately to the number of simultaneous slice acquisitions (which we denote by R ). While preliminary results in [6, 16] showed good reproducibility, yet the effect of simultaneous acquisitions on long range fiber connectivity and diffusion measures such as FA, is not known. In this work, we use multi-tensor based fiber connectivity to compare data acquired on two subjects with different acceleration factors ( R = 1, 2, 3). We investigate and report the reproducibility of fiber bundles and diffusion measures between these scans on two subjects with different spatial resolutions, which is quite useful while designing neuroimaging studies.
Introduction
High Angular Resolution Diffusion Imaging (HARDI) involves acquiring diffusion information for a single b-value in several gradient directions uniformly spread on a sphere [] can greatly increase the speed of the EPI encoding by eliminating phase encoding steps. Although beneficial for other reasons, this does not translate to a significant reduction in TR or acquisition time, as diffusion sequences contain large, fixed time blocks that cannot be shortened, such as the time for diffusion encoding or the time to a suitable echo time (TE) for T2* contrast.
In comparison, accelerating the data acquisition using the simultaneous acquisition of multiple slices can be very effective as it directly reduces the amount of time needed to acquire a fixed number of slices. For example, if three imaging slices are acquired per shot instead of one, the total acquisition time decreases directly by a factor of 3. When TR>T1, then the acquisition can maintain a nearly fully relaxed equilibrium magnetization even for three acceleration. Furthermore, unlike standard parallel imaging techniques, simultaneous multi-slice acquisition methods do not shorten the readout period or omit k-space samples. Therefore, they are not subject to a
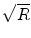
penalty on SNR (where R is the acceleration factor) found in conventional parallel imaging acceleration. Thus, in this work, we use the multi-slice acquisition protocol detailed in [], which uses both the inplane (acceleration factor of 2) and slice accelerations to simultaneously acquire data from multiple slices. In this case, the repetition time TR is reduced proportionately to the number of multi-slice acquisitions R .
Our Contributions
We propose to quantitatively compare three different multi-slice acquisition schemes corresponding to the acceleration factors of R ={ 1,2,3} respectively. Existing work in [] to obtain full brain connectivity and quantitatively compare fiber bundles from different acquisitions. We also compare the effect of spatial resolution on diffusion measures (FA and trace) and fiber bundle connectivity for the three acceleration factors. Thus, to the best of our knowledge, this is a first such quantitative study on comparing multi-slice acquisitions. Knowing the performance of each type of scan can provide useful information during the design of neuroimaging studies.
Methods
Multi-tensor analysis: It is now quite well-known that the single tensor method is inadequate for representing multi-fiber compartments [], adding an isotropic free-water component to the model can better characterize the signal and produces more accurate fiber tracts. We thus use two-tensors and an isotropic free-water compartment to model our signal S :
where,
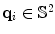
is the gradient direction,
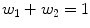
and w i forms the volume fraction of each component, D 1 and D 2 are cylindrical tensors and D iso is an isotropic tensor with fixed diffusivity of 0.003mm2s as given in [).
Metric for comparing fiber bundles: Several metrics have been proposed to compute distances (overlap) between fiber bundles, in the context of fiber bundle registration []. Then, the Bhattacharyya metric in the x-coordinate B x is given by:
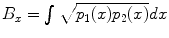
, where p 1( x ), p 2( x ) are the pdfs to be compared. To compute the distance between two fiber bundles, we simply take an equally-weighted combination in each co-ordinate:
Note that, if p 1= p 2, then
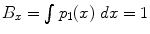
. Thus, values of B are bounded between 0 and 1. Further, B will be 1 for a perfect match between two fiber bundles and 0 for no overlap at all.
Experiments
Data acquisition: We acquired diffusion MRI data on two subjects using the following set of parameters and an in-plane acceleration factor of 2: (1) For subject # 1, we used the following scan parameters: 60 gradient directions at a b-value of 1,000, (echo time) TE=130 ms, spatial resolution of 2 2 2=8mm3. Three data sets were acquired for three acceleration factors R ={ 1,2,3} with repetition time TR={10.6, 5.5, 3.7}s respectively. (2) For subject # 2, all parameters were the same, except the spatial resolution, which was 2.5 2.5 2.5=15.62mm3. A decrease in the spatial resolution from 8 to 15.62mm3 increases the SNR by a factor of 2 (proportional to the increase in size of the voxel
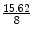













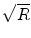 penalty on SNR (where R is the acceleration factor) found in conventional parallel imaging acceleration. Thus, in this work, we use the multi-slice acquisition protocol detailed in [], which uses both the inplane (acceleration factor of 2) and slice accelerations to simultaneously acquire data from multiple slices. In this case, the repetition time TR is reduced proportionately to the number of multi-slice acquisitions R .
penalty on SNR (where R is the acceleration factor) found in conventional parallel imaging acceleration. Thus, in this work, we use the multi-slice acquisition protocol detailed in [], which uses both the inplane (acceleration factor of 2) and slice accelerations to simultaneously acquire data from multiple slices. In this case, the repetition time TR is reduced proportionately to the number of multi-slice acquisitions R .
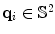 is the gradient direction,
is the gradient direction, 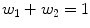 and w i forms the volume fraction of each component, D 1 and D 2 are cylindrical tensors and D iso is an isotropic tensor with fixed diffusivity of 0.003mm2s as given in [).
and w i forms the volume fraction of each component, D 1 and D 2 are cylindrical tensors and D iso is an isotropic tensor with fixed diffusivity of 0.003mm2s as given in [).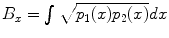 , where p 1( x ), p 2( x ) are the pdfs to be compared. To compute the distance between two fiber bundles, we simply take an equally-weighted combination in each co-ordinate:
, where p 1( x ), p 2( x ) are the pdfs to be compared. To compute the distance between two fiber bundles, we simply take an equally-weighted combination in each co-ordinate: 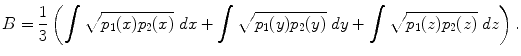
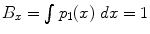 . Thus, values of B are bounded between 0 and 1. Further, B will be 1 for a perfect match between two fiber bundles and 0 for no overlap at all.
. Thus, values of B are bounded between 0 and 1. Further, B will be 1 for a perfect match between two fiber bundles and 0 for no overlap at all.