Taeyoung Lee Melvin Leok - Global formulations of Lagrangian and Hamiltonian dynamics on manifolds: a geometric approach to modeling and analysis

Global formulations of Lagrangian and Hamiltonian dynamics on manifolds: a geometric approach to modeling and analysis — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Global formulations of Lagrangian and Hamiltonian dynamics on manifolds: a geometric approach to modeling and analysis" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...254

Springer International Publishing AG 2018

Taeyoung Lee , Melvin Leok and N. Harris McClamroch Global Formulations of Lagrangian and Hamiltonian Dynamics on Manifolds Interaction of Mechanics and Mathematics

1. Mathematical Background

Taeyoung Lee 1, Melvin Leok 2 and N. Harris McClamroch 3

(1)

The George Washington University, Washington, District of Columbia, USA

(2)

Department of Mathematics, University of California, San Diego, La Jolla, California, USA

(3)

Department of Aerospace Engineering, The University of Michigan, Ann Arbor, Michigan, USA

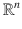Dynamical systems are most naturally described in the language of differential equations. For many, but not all dynamical systems, the variables that describe the motion dynamics can be viewed as elements of a finite-dimensional vector space , e.g., . But there are important situations where the variables that describe the dynamics do not lie in a vector space but rather lie in a set with a different mathematical structure, in particular a manifold structure. In this case, the solution flow of the differential equations that describe the dynamics of the system must evolve on this manifold.

In this chapter, we summarize the mathematical background that is used subsequently. Important results in linear algebra are introduced for finite-dimensional vectors and matrices viewed as linear transformations. A summary is given of manifold concepts and related differential geometric concepts are introduced; a summary of results for vector fields on a manifold is given. Further mathematical background is presented in Chapter , where additional details on Lie groups and homogeneous manifolds are provided. That material appears there since it is not required for the prior developments .

1.1 Vectors and Matrices

A vector is an n -tuple of real numbers. Vector addition and scalar multiplication are defined as usual. A matrix is an n m ordered array of real numbers. Matrix addition, for compatible matrices, and scalar multiplication are defined as usual.

The transpose of an n m matrix A is an m n matrix, denoted by A T , obtained by interchange of the rows and columns. The n n identity matrix is denoted by I n n . The n m zero matrix composed of zero elements is denoted by 0 n m or more often by 0.

Vector spaces in this book should be understood as being defined over the real field ; the only exception occurs when we occasionally use eigenvalue and eigenvector concepts, in which case the field is the complex field . An excellent reference on matrix theory is [] .

1.1.1 Vector Spaces

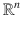As usual, denotes the set of all ordered n -tuples of real numbers, with the usual definition of vector addition and scalar multiplication. Thus, 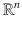is a real vector space. Also, 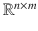denotes the set of all n m real matrices consisting of n rows and m columns. With the usual definition of matrix addition and scalar multiplication of a matrix, 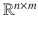is a real vector space. Unless indicated otherwise, we view an n -tuple of real numbers as a column vector and we view a matrix as an array of real numbers.

The common notions of span , linear independence , basis , and subspace are fundamental. The dimension of a vector space is the number of elements in a basis.

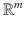Linear transformations can be defined from the vector space to the vector space 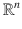; such a linear transformation can be represented by a real matrix in 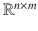. Linear transformations from a vector space to the vector space 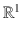are referred to as linear functionals .

We also make use of common matrix notions of rank , determinant , singular matrix , and eigenvalues and eigenvectors .

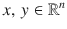The usual Euclidean inner product or dot product of two vectors is the real number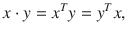

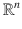(1.1)

and the Euclidean norm on the real vector space is the nonnegative real number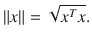

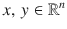(1.2)

Vectors that satisfy x y = 0 are said to be orthogonal or normal. If 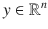is nonzero, then the set of vectors that are orthogonal to y is referred to as the orthogonal complement of y ; the orthogonal complement is an ( n 1)-dimensional subspace of .

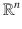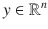Suppose that a vector is nonzero, then a vector can be uniquely decomposed into the linear combination of a vector in the direction of 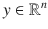and a vector orthogonal to 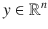; this is given by the expression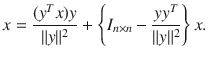

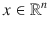(1.3)

The first term on the right is the component of in the direction of 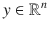, referred to as the orthogonal projection of x onto y . The second term on the right is the component of 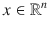orthogonal to

Next page

1234567...254

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Global formulations of Lagrangian and Hamiltonian dynamics on manifolds: a geometric approach to modeling and analysis»

Look at similar books to Global formulations of Lagrangian and Hamiltonian dynamics on manifolds: a geometric approach to modeling and analysis. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Melvin L. Kohn

Change and Stability: A Cross-National Analysis of Social Structure and Personality

Banavara N. Shashikanth

Dynamically Coupled Rigid Body-Fluid Flow Systems

Frank Nielsen (editor)

Progress in Information Geometry: Theory and Applications

Paolo Ciatti

Geometric Aspects of Harmonic Analysis

Nickolay Trendafilov

Multivariate Data Analysis on Matrix Manifolds: (with Manopt)

Steven G. Krantz

Geometric Analysis of the Bergman Kernel and Metric

Spivak

Calculus on manifolds: a modern approach to classical theorems of advanced calculus

Epstein

Differential geometry: basic notions and physical examples

Claudio Gorodski

Smooth Manifolds

Swaters

Introduction to Hamiltonian Fluid Dynamics and Stability Theory

V. I. Arnold

Mathematical Methods of Classical Mechanics

Melvin Hausner

A Vector Space Approach to Geometry

Discussion, reviews of the book Global formulations of Lagrangian and Hamiltonian dynamics on manifolds: a geometric approach to modeling and analysis and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.