Cohen - Linear Algebra: Intuition, Math, Code

Linear algebra Linear algebra has a long history in pure mathematics, in part because it provides a compact notation that is powerful and general enough to be used in geometry, calculus, differential equations, physics, economics, and many other areas.

1 FACT :
Linear algebra is
SUUUUPER
IMPORTANT!!

But the importance and application of linear algebra is quickly increasing in modern applications. Many areas of science, technology, finance, and medicine are moving towards large-scale data collection and analysis. Data are often stored in matrices, and operations on those dataranging from statistics to filtering to machine learning to computer graphics to compressionare typically implemented via linear algebra operations. Indeed, linear algebra has arguably exceeded statistics and time series analysis as the most important branch of mathematics in which to gain proficiency for data-focused areas of science and industry.

Human civilization is moving towards increasing digitization, quantitative methods, and data. Therefore, knowledge of foundational topics such as linear algebra are increasingly important. One may (indeed: should ) question the appropriateness and utility of the trend towards "big data" and the over-reliance on algorithms to make decisions for us, but it is inarguable that familiarity with matrix analysis, statistics, and multivariate methods have become crucial skills for any data-related job in academia and in industry.

The purpose of this book is to teach you how to think about and work with matrices, with an eye towards applications in machine learning, multivariate statistics, time series, and image processing. If you are interested in data science, quantitative biology, statistics, or machine learning and artificial intelligence, then this book is for you. If you dont have a strong background in mathematics, then dont be concerned: You need only high-school math and a bit of dedication to learn linear algebra from this book.

This book is written with the self-studying reader in mind. Many people do not realize how important linear algebra is until after university, or they do not meet the requirements of university-level linear algebra courses (typically, calculus). Linear algebra textbooks are often used as a compendium to a lecture-based course embedded in a traditional university math program, and therefore can be a challenge to use as an independent resource. I hope that this book is a self-contained resource that works well inside or outside of a formal course.

Many extant textbooks are theory-oriented, with a strong focus on abstract concepts as opposed to practical implementations. You might have encountered such books: They avoid showing numerical examples in the interest of generalizations; important proofs are left "as an exercise for the reader"; mathematical statements are simply plopped onto the page without discussion of relevance, importance, or application; and there is no mention of whether or how operations can be implemented in computers.

I do not write these as criticismsabstract linear algebra is a beautiful topic, and infinite-dimensional vector spaces are great. But for those interested in using linear algebra (and mathematics more generally) as a tool for understanding data, statistics, deep learning, etc., then abstract treatments of linear algebra may seem like a frustrating waste of time. My goal here is to present applied linear algebra in an approachable and comprehensible way, with little focus on abstract concepts that lack a clear link to applications.

Ebook version The ebook version is identical to the physical version of this book, in terms of the text, formulas, visualizations, and code. However, the formatting is necesarily quite different. The book was designed to be a physical book; and thus, margins, fonts, text and figure placements, and code blocks are optimized for pages, not for ereaders.

Therefore, I recommend getting the physical copy of the book if you have the choice. If you get the ebook version, then please accept my apologies for any ugly or annoying formatting issues. If you have difficulties reading the code, please download it from github.com/mikexcohen/LinAlgBook.

Equations This is a math book, so you wont be surprised to see equations. But math is more than just equations: In my view, the purpose of math is to understand concepts; equations are one way to present those concepts, but words, pictures, and code are also important. Let me outline the balance:

1.Equations provide rigor and formalism, but they rarely provide intuition.2.Descriptions, analogies, visualizations, and code provide intuition but often lack sufficient rigor.

This balance guides my writing: Equations are pointless if they lack descriptions and visualizations, but words and pictures without equations can be incomplete or misinterpreted.

So yes, there is a respectable number of equations here. There are three levels of hierarchy in the equations throughout this book. Some equations are simple or reminders of previously discussed equations; these are lowest on the totem pole are are presented in-line with text like this: x ( yz ) = ( xy ) z .

More important equations are given on their own lines. The number in parentheses to the right will allow me to refer back to that equation later in the text (the number left of the decimal point is the chapter, and the number to the right is the equation number).

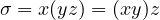(1.1)

And the most important equationsthe ones you should really make sure to understand and be comfortable using and reproducingare presented in their own box with a title:
__________________________________________________________________

Eqn. box title= Something important!

= x ( yz ) = ( xy ) z

(1.2)

__________________________________________________________________

Algebraic and geometric perspectives on matrices Many concepts in linear algebra can be formulated using both geometric and algebraic (analytic) methods. This "dualism" promotes comprehension and I try to utilize it often. The geometric perspective provides visual intuitions, although it is usually limited to 2D or 3D. The algebraic perspective facilitates rigorous proofs and computational methods, and is easily extended to N-D. When working on problems in or , I recommend sketching the problem on paper or using a computer graphing program.

Just keep in mind that not every concept in linear algebra has both a geometric and an algebraic concept. The dualism is useful in many cases, but its not a fundamental fact that necessarily applies to all linear algebra concepts.

The obvious . Dare I write it? You need to be motivated to learn linear algebra. Linear algebra isnt so difficult, but its also not so easy. An intention to learn applied linear algebraand a willingness to expend mental energy towards that goalis the single most important prerequisite. Everything below is minor in comparison.

High-school math . You need to be comfortable with arithmetic and basic algebra. Can you solve for x in x = 9 ? Then you have enough algebra knowledge to continue. Other concepts in geometry, trigonometry, and complex numbers ( a ib,e i ) will be introduced as the need arises.

Calculus . Simply put: none. I strongly object to calculus being taught before linear algebra. No offense to calculus, of course; its a rich, beautiful, and incredibly important subject. But linear algebra can be learned without any calculus, whereas many topics in calculus involve some linear algebra. Furthermore, many modern applications of linear algebra invoke no calculus concepts. Hence, linear algebra should be taught assuming no calculus background.