Michael Batty
Essential Group Theory
Essential Group Theory
2015 Michael Batty & bookboon.com ISBN 978-87-403-0301-8
Contents
Introduction 9
1 Sets and Maps
1.1 Sets
1.2 Maps
1.3 Equivalence Relations and Partitions
1.4 Modular Arithmetic
10
11
12
13
2 Groups
2.1 Binary Operations
2.2 Groups: Basic Definitions
2.3 Examples of Groups
14
15
17
3 Subgroups
3.1 Definition of a Subgroup
3.2 Cosets
3.3 Lagranges Theorem
I joined MITAS because
I wanted
real responsibili
I joined MITAS because
21
22
23
Real work
International opportunities
ree woorree work placements
Month 16 I was a construction Month 16
supervisor in I was a construction the North Sea advising and helping foremen
supervisor the North Sea advising
solve problems helping for International opportunities
ree work placements solve problems
WHY WAIT FOR PROGRESS?
DARE TO DISCOVER
Discovery means many different things at
Schlumberger. But its the spirit that unites every
single one of us. It doesnt matter whether they
join our business, engineering or technology teams,
our trainees push boundaries, break new ground
and deliver the exceptional. If that excites you,
then we want to hear from you.
careers.slb.com/recentgraduates

13 Free Groups
13.1 Reduced Words and Free Groups
13.2 Normal Closure
13.3 Torsion Free Groups
60
61
62
14 Abelian Groups
14.1 Commutator Subgroups and Abelianisations
14.2 Free Abelian Groups
14.3 Finitely Generated Abelian Groups
14.4 Generalisations of Abelian Groups
64
65
67
67
15 Transforming Presentations
15.1 Tietze Transformations
15.2 Properties of Tietze Transformations
69
71
16 Free Products
16.1 Free Products
16.2 A Normal Form for Free Products
16.3 The Universal Property of Free Products
16.4 Independence of Presentation
16.5 Decomposability
74
76
77
78
78
PREPARE FOR A LEADING ROLE.
English-taught MSc programmes in engineering: Aeronautical, Biomedical, Electronics,
Mechanical, Communication systems and Transport systems. No tuition fees.
E liu.se/master
17 Free Products With Amalgamation 80
17.1 Free Products with Amalgamation 80
17.2 Pushouts 81
17.3 Independence of Presentation 85
18 HNN Extensions 86
18.1 HNN Extensions 86
18.2 Relation to Free Products with Amalgamation 87
18.3 The Higman-Neumann-Neumann Embedding Theorem 90
19 Further Reading 92
20 Bibliography 94
21 Index 95
Click here to learn more
TAKE THE
RIGHT TRACK
Give your career a head start
by studying with us. Experience the advantages of our collaboration with major companies like ABB , Volvo and Ericsson !
Apply by 15 January World class www.mdh.se research

Essential Group Theory Introduction
Introduction
This short book on group theory is partly based on notes from lectures I gave at Trinity College Dublin in 1999 and at Edinburgh University in 2001. The first part of the book is an introduction to elementary group theory. It doesnt aim to cover everything that might be in your introductory course in abstract algebra, but just to give a summary of the important points. Perhaps you could read it before you begin your course, if you want to read something gentle in advance, or it could be a starting point for revision. The second part of the book is about free groups and presentations of groups. This would typically appear in a second course on group theory.
Group theory can seem very abstract and strange when you first encounter it. It involves a different mindset and most likely you will not have done this type of mathematics before. But it has a set of
techniques and beauty of its own and is worth perservering with, and you will find that the Gs and
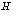
s will soon come to life.
As with a lot of university mathematics, it depends very much on the language and logic of sets and their elements, containment, equality and maps and unless you understand these fully, it is unlikely that you will be able to apply them in the context of group theory, where there is even more to think about. Most of the elementary proofs in group theory involve these simple but important techniques. I cant stress this enough and have included a preliminary section on sets and maps before the main theme of group theory starts.











 e Graduate Programme
e Graduate Programme















 www.job.oticon.dk
www.job.oticon.dk

 Essential Group Theory Introduction
Essential Group Theory Introduction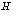 s will soon come to life.
s will soon come to life.